2022AIME美國數學競賽邀請賽及歷年真題下載
AIME由AMC10和AMC12的優勝者參加，參加標準為：AMC10全球前2.5%或AMC12全球前5%，具體晉級比例每年根據參賽人數的比賽結果會有所變化。
AIME是介于AMC10、AMC12及美國數學奧林匹克學術活動（USAMO）之間的一個數學學術活動，主要目的是結合AMC10和12的成績篩選出晉級USAMO的選手，進而通過下一步的比賽與暑期集訓（MOP）選拔出6位最終參加IMO（國際數學奧林匹克）的美國國家隊成員。學術活動開始于1983年。2000年起AIME增加一場比賽，分為AIME I和AIME II兩場。
2022AIME I 真題及答案
翰林學院整理了1983年來全部AIME真題及解答
（下載方式見文末）
AIME比賽時間在2021年之前為每年的3月中旬與三月底，2021年秋季改制之后，自2022年起為每年的2月中旬與下旬分別舉行I卷與II卷的考試。
AIME的考題相對于AMC10及AMC12而言更具難度，給晉級的學生提供了更進一步的挑戰和數學能力水平認證的可能。
AIME成績優異的具有美國身份的學生將再被邀請參加USJMO和USAMO數學學術活動，對于非美國籍的學生，AIME就是AMC系列比賽選拔的終點，但在數學方面有優異才能的學生，也可以通過與其他參賽選手獲得的成績進行對比對自己的數學能力得到肯定。
考試形式
AIME學術活動考試時間為3小時，一共15道填空題，一題一分，滿分15分，每題的得分只看最后答案是否正確而不需要提供解答的過程，比賽中不允許使用計算器。AIME問題的難度會隨著題目編號的增加而逐漸加大，其前面大部分題目和AMC12最后十題的難度基本相當，最后三道題一般會均有相當的挑戰性，甚至達到olympiad入門題目的水平。
考試安排
AIME目前在每年2月中旬與下旬舉辦。
考試內容
AIME 的考試內容基本與AMC12相當，但在數論、代數、幾何、組合各個核心板塊中有進一步的加深和拓展。比如數論部分主要引入了少量olympiad級別比賽涉及到的概念與結果，比如階和原根的概念，中國剩余定理的熟練應用，Wilson定理、LTE升冪引理的應用。
代數部分顯著增加了題目的運算量，包括復雜三角恒等式（和差化積，積化和差，三角形內的三角恒等式）的運用，高斯函數相關問題的考察，以及復數、向量等工具在數形結合問題中的應用。
幾何部分同樣顯著增加了題目的運算量，三角工具、坐標工具、復數工具在幾何題目解決過程中的重要性進一步增加，同時部分較難題目適當引入了入門級別olympiad題目的常見幾何構型，對于晉級到下一輪MO的選手熟悉、學習相關專業內容起到一個承接的作用。組合部分的題目加大了對于遞歸方法的應用，復雜容斥原理的應用以及與其他板塊交叉、具有復合背景的計數問題的考察。
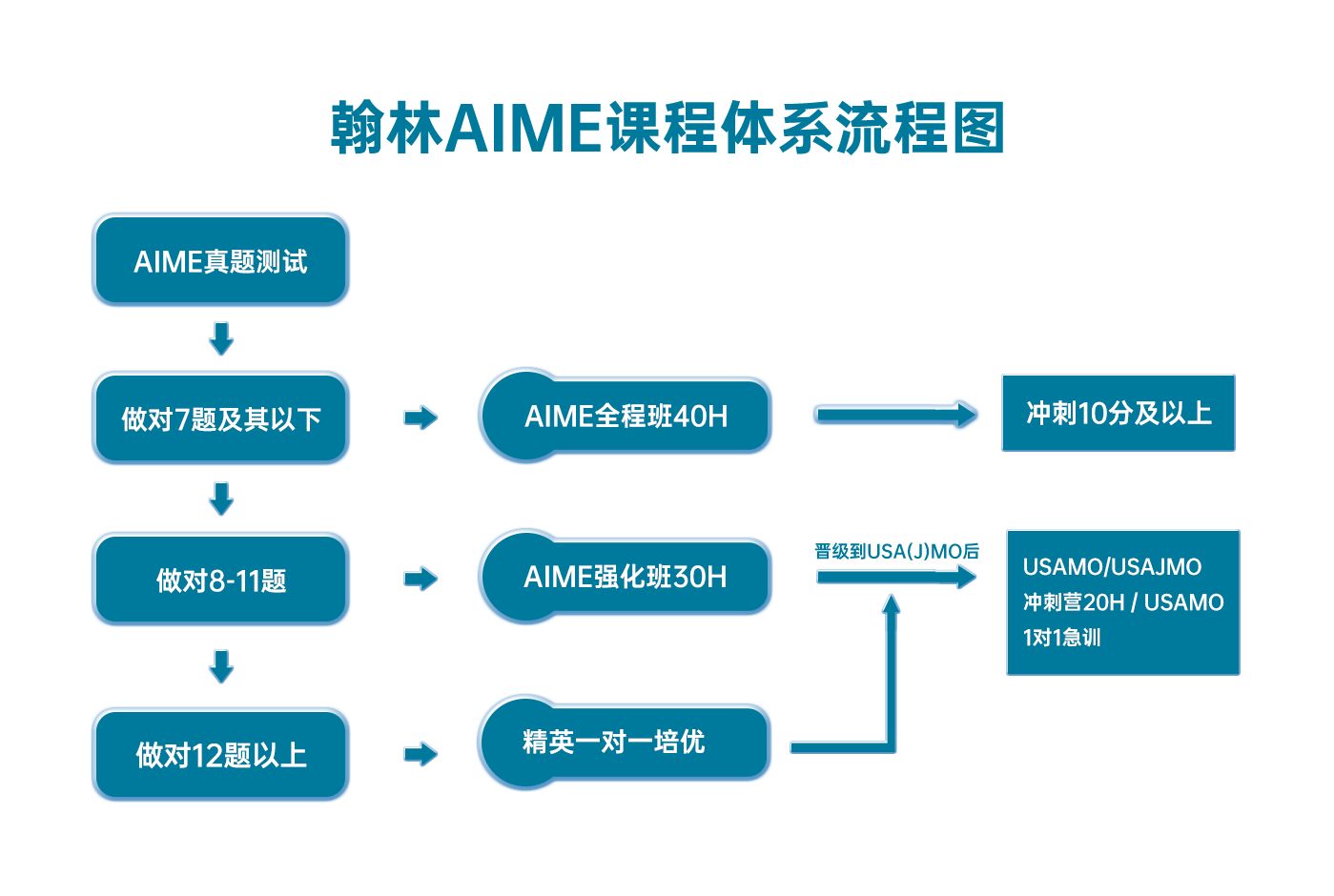
翰林AIME課程體系流程圖
翰林為AMC數學競賽【官方授權考點】，可提供賽事報名
掃碼聯系小助手領取報名表
國際競賽真題資源免費領取
美高學分項目重磅來襲！立即了解
