 測試評估
測試評估
精準評估水平
分級系統教學
翰林作為社會考點,可協助社會考生進行報名,翰林已連續多年累計為幾千名學生安排AMC考試。
- 翰林AMC8在讀學員可免費報名
- 考試報名贈送AMC8資料包
- 前100名報名的學生可贈送999元AMC8備考管家課程
翰林教育AMC8課程,專為3-6年級青少年量身打造。我們構建了科學完善的教學服務體系,為學生鋪設通向優異成績的堅實路徑。從課前評估到課后輔導,從考前模擬到報名服務我們致力于為孩子提供全方位的學習支持。
翰林教育AMC8課程不僅追求優異的競賽成績,更著眼于學生長遠數學素養的培養。通過系統的思維訓練和能力提升,我們致力于為學員打下扎實的數學基礎,培養其邏輯思維能力和創新意識,為其未來的數學學習和學術發展奠定堅實基礎。
AMC8競賽介紹
AMC8(American Mathematics Competition8)由美國數學協會(MAA)專為全球8年級及以下學生舉辦的數學競賽,有些小學四~六年級的優秀學生也可以參加,該競賽開始于1985年。
自2006年起,AMC8競賽正式引入中國,其影響力在此后的年份里逐漸增強,吸引了越來越多的學生參與。隨著時間的推移,參賽人數逐年攀升,這也體現了中國學生對數學競賽的熱情和對挑戰的渴望。如今,AMC8競賽在中國已成為備受關注的數學競賽之一,其含金量和影響力在小初階段尤為顯著。
課前籌備-課中精研-課后督導-考前服務-長效優化
 測試評估
測試評估精準評估水平
分級系統教學
 貼心服務
貼心服務紙制自研教材
每次課前提醒
 高效提升
高效提升精品小班教學
高效突破提升
 學情反饋
學情反饋課后及時反饋
家長掌握學情
 鞏固提升
鞏固提升督促作業完成
助教答疑輔導
 復習沖刺
復習沖刺贈送考前模考班課
模擬試卷訓練提升
 無憂保障
無憂保障提供賽事報名服務
在線或者線下考試
 服務迭代
服務迭代結課收集學員評價
不斷提升課程質量
 課程設置
課程設置基礎強化全程班型
滿足不同年齡基礎
| 知識模塊 | 課程內容 | 課時 |
|---|---|---|
| 1. Exponents-冪的認識與運算 | Squares and Cubes 平方和立方 | 6H |
| Higher Exponents 高次冪的運算 | ||
| Zero and Negative Exponents 零次冪與負次冪 | ||
| From Squares to Square Roots 平方與平方根 | ||
| Square Roots of Non-square Integers 非平方數的平方根 | ||
| Arithmetic with Square Roots 平方根的運算 | ||
| 2. Number Theory-數論 | Multiples and Divisor 倍數與除數 | 4H |
| Divisibility 整除 | ||
| Prime Numbers and Prime Factorization 質數與質因數分解 | ||
| LCM and GCF 最大公因數和最小公倍數 | ||
| 3. Fractions-分數 | Multiplying and Dividing by a Fraction 分數的乘除法 | 9H |
| Raising Fractions to Powers 分數的冪運算 | ||
| Simplest Form of a Fraction 分數化簡 | ||
| Comparing Fractions 分數比較大小 | ||
| Adding and Subtracting Fractions 分數加減 | ||
| Mixed Numbers 帶分數 | ||
| Percepts 百分數 | ||
| Percent Increase and Decrease增長與降低百分比 | ||
| Word Problems 相關應用題 | ||
| 4. Decimals-小數 | Arithmetic with Decimals 小數運算 | 2H極 |
| Rounding 估算與近似 | ||
| Decimals and Fractions 小數與分數的轉換 | ||
| 5. Equations and Inequalities-方程與不等式 | Expressions 代數式 | 4H |
| Solving Linear Equations 一次方程 | ||
| Word Problems 相關應用題 | ||
| Inequalities 不等式 | ||
| 6. Ratios, Conversions, and Rates-比例與比率 | Ratios 比例 | 5H |
| Proportions 等價比例(分數) | ||
| Conversions 轉換率 | ||
| Speed 行程問題 | ||
| Other Rates 其他比率問題 | ||
| 7. Angles-角度 | Parallel Lines 平行線 | 4H |
| Angles in a Triangle 角度與三角形 | ||
| Exterior Angles 外角 | ||
| Angles in Polygons 角度與多邊形 | ||
| 8. Triangles-三角形 | Congruence 全等 | 9H |
| Isosceles and Equilateral Triangles 等腰與等邊三角形 | ||
| The Pythagorean Theorem 勾股定理 | ||
| Some Special Triangles 特殊三角形 | ||
| Similar Triangles 相似三角形 | ||
| Perpendicular Bisectors of a Triangle 三角形的垂直平分線 | ||
| Medians and Altitudes 中線與高 | ||
| 9. Quadrilaterals-四邊形 | Trapezoids 梯形 | 3H |
| Parallelograms 平行四邊形 | ||
| Rhombi 菱形 | ||
| Rectangles 長方形 | ||
| Squares 正方形 | ||
| 10. Circles-圓 | Arc Measure, Arc Length, and Circumference 弧長與周長 | 4H |
| Area 面積 | ||
| Funky Areas 特殊部分面積 | ||
| Tangents 相切 | ||
| 11. Three-Dimensional Geometry-立體幾何 | Prisms 棱柱 | 2H |
| Pyramids 錐形 | ||
| Regular Polyhedron 多面體 | ||
| 12. Data and Statistics-數據統計 | Basic Statistics 統計基礎 | 2H |
| Tables, Graphs, and Charts 表格與統計圖 | ||
| Sets 集合 | ||
| 13. Counting-計數 | Counting with Addition and Subtraction 加法原理 | 6H |
| The Multiplication Principle 乘法原理 | ||
| Casework 分類討論 | ||
| Counting Pairs 計數成對項 | ||
| Probability 概率 |
本課程適合校內基礎扎實并想要參加AMC 8競賽并沖擊前5%及以上獎項的學生。
| 知識模塊 | 分支模塊 | 課程內容 | 課程時長 |
|---|---|---|---|
| Number Theorem-數論 | ①factors and prime factorizations-質因數分解 | Factors因數 | 8H |
| Divisors除數 | |||
| Power冪 | |||
| Composite number合數 | |||
| Prime number質數 | |||
| The Square Root Rule 平方根規則 | |||
| Relatively prime互質 | |||
| Prime Factorizations質因數分解 | |||
| Square平方數 | |||
| Cube立方數 | |||
| Number of divisors 因數個數 | |||
| GCD and LCM 最大公因數和最小公倍數 | |||
| ②Even, Odd and Divisibility-奇偶性,整除技巧 | Even and Odd 奇數和偶數 | ||
| Divisibility 整除 | |||
| ③Base Number and Digits-進制與位值 | Base 10 number representations 十進制表達 | ||
| Remainder 余數 | |||
| Algebra-代數 | Sequences and Series-數列與求和 | Arithmetic sequence 等差數列 | 8H |
| Geometric sequences等比數列 | |||
| Ratios, Rates, and Proportions-比率與比例 | Ratios 比率 | ||
| Proportions比例 | |||
| Continued Ratio 連比 | |||
| Speed 速度 | |||
| Equation and Inequalities-方程與不等式 | Fundamental law of fractions 分數的基本法則 | ||
| Power rules of exponents 指數的冪法則 | |||
| Properties of radicals 根式的性質 | |||
| Properties of absolute value 絕對值的性質 | |||
| Square binomial 二項展開式(二次方)和平方差 | |||
| One-variable Linear Equations 一元一次方程 | |||
| Quadratic Equations二次方程的解 | |||
| Linear Inequalities 一次不等式 | |||
| Sets and Venn diagram-集合與韋恩圖 | Set集合 | ||
| Mid-term Review-階段復習 | Mid-term Test-期中測試 | 2H | |
| Mid-term Review-階段復習與總結 | |||
| Geometry-幾何 | Triangles and Similarity-三角形與相似性 | Areas of Triangle三角形面積 | 9H |
| Triangle Inequality Theorem三角不等式 | |||
| PYTHAGOREAN THEOREM 勾股定理 | |||
| Similar triangles相似三角形 | |||
| Polygons-多邊形 | Polygons多邊形 | ||
| The Pick’s Law皮克定理 | |||
| Circles-圓 | Circumference and Area of Circle圓的周長與面積 | ||
| Area of sector 扇形的面積 | |||
| Length of the arc 扇形的弧長 | |||
| Volumes-體積 | Rectangular solid 長方體 | ||
| Triangular prism 三棱柱 | |||
| Cylinder 圓柱 | |||
| Cone 圓錐 | |||
| Pyramid 棱錐 | |||
| Octahedron 八面體 | |||
| Probability and Statistic-統計與概率 | Statistics-統計 | Mean Median Mode and Range平均數,中位數,眾數和極差 | 9H |
| Factorial 階乘 | |||
| Permutations and Combinations-排列組合 | Permutation 排列 | ||
| Combination 組合 | |||
| Circular Permutations循環排列 | |||
| Probability-概率 | Probability概率 | ||
| Practice and Review-復習與練習 | Past Paper Practice 近5年真題練習講解與分析 | 4H | |
卓越之師,專業筑夢。以深厚的學識與滿腔熱忱,引領孩子綻放無限可能。



美國內布拉斯加林肯大學碩士,曾在南美、歐洲多個國家及英國參與交流項目。熟悉不同的教育體系,并在數學教學領域擁有多年的豐富實踐經驗,對國際主流數學競賽了如指掌。



新加坡國立大學量化金融碩士,本科畢業于南方科技大學數學系,多年海外經歷,多次獲得國家、校獎學金,熟悉不同國家教學體系及風格、三大國際課程體系及國際主流數學競賽。



英國南安普敦大學管理科學博士,英國蘭卡斯特大學運籌學碩士,上海華東師范大學物理學士。具備扎實的數理基礎,讀博期間擔任大學助教,教授大學一二年級數學統計等課程。







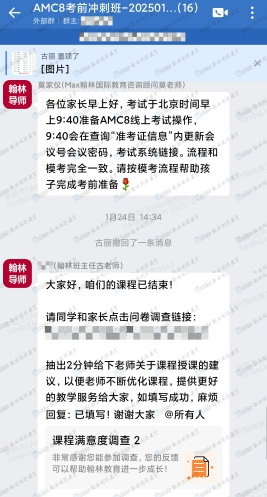
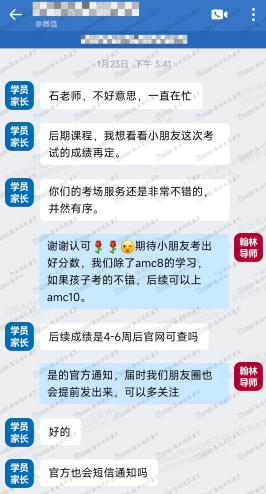
AMC8數學競賽熱點資訊
在當今競爭激烈的學生時代,數學競賽已成為許多學生展示自我、提升競爭力的重要舞臺。AMC8作為一項備受矚目的國際數學競賽,不僅考驗學生的數學素養,還鍛煉他們解決實際問題的能力。本文將深入剖析AMC8的難度、...
More隨著國際教育競爭日益激烈,AMC8數學競賽已成為眾多學生展示數學能力的重要平臺。然而,許多家長和學生面臨這樣的困惑:AMC8競賽究竟考什么?難度如何?如何科學備考才能在競爭中脫穎而出?本文將為您詳細解析AMC...
More隨著國際數學競賽的熱潮不斷升溫,AMC8作為其中的佼佼者,受到了越來越多家長和學生的關注。那么,AMC8究竟相當于什么水平?幾年級的學生更適合參加?本文將為你詳細解讀AMC8競賽的相關內容,助你輕松應對挑戰。 ...
More隨著全球教育競爭加劇,AMC8(美國數學競賽8年級組)逐漸成為國內家長圈的熱議話題。數據顯示,近年參賽人數激增,低齡化趨勢顯著——三年級學生占比突破20%,而上海"三公"學校錄取者中,超80%持有優異的AMC8成績單...
More隨著教育國際化的不斷深入,AMC8數學競賽逐漸成為國內外家長和學生關注的焦點。近年來,AMC8競賽呈現出明顯的低齡化趨勢,越來越多的小學生在三年級甚至更早就開始備戰這一賽事。那么,AMC8競賽究竟有何魅力?它...
More