- 翰林提供學術(shù)活動、國際課程、科研項目一站式留學背景提升服務(wù)!
- 400 888 0080
2006 AMC12A 真題及答案詳細解析
2006 AMC 12 A 真題
答案詳細解析請參考文末
Problem 1
Sandwiches at Joe's Fast Food cost?![]() ?dollars each and sodas cost?
?dollars each and sodas cost?![]() ?dollars each. How many dollars will it cost to purchase?
?dollars each. How many dollars will it cost to purchase?![]() ?sandwiches and?
?sandwiches and?![]() sodas?
sodas?
![]()
Problem 2
Define?![]() . What is?
. What is?![]() ?
?
![]()
Problem 3
The ratio of Mary's age to Alice's age is?![]() . Alice is?
. Alice is?![]() ?years old. How old is Mary?
?years old. How old is Mary?
![]()
Problem 4
A digital watch displays hours and minutes with AM and PM. What is the largest possible sum of the digits in the display?
![]()
Problem 5
Doug and Dave shared a pizza with?![]() ?equally-sized slices. Doug wanted a plain pizza, but Dave wanted anchovies on half the pizza. The cost of a plain pizza was?
?equally-sized slices. Doug wanted a plain pizza, but Dave wanted anchovies on half the pizza. The cost of a plain pizza was?![]() ?dollars, and there was an additional cost of?
?dollars, and there was an additional cost of?![]() ?dollars for putting anchovies on one half. Dave ate all the slices of anchovy pizza and one plain slice. Doug ate the remainder. Each paid for what he had eaten. How many more dollars did Dave pay than Doug?
?dollars for putting anchovies on one half. Dave ate all the slices of anchovy pizza and one plain slice. Doug ate the remainder. Each paid for what he had eaten. How many more dollars did Dave pay than Doug?
![]()
Problem 6
The?![]() ?rectangle?
?rectangle?![]() ?is cut into two congruent hexagons,?as?shown, in such a way that the two hexagons can be repositioned without overlap to form a square. What is?
?is cut into two congruent hexagons,?as?shown, in such a way that the two hexagons can be repositioned without overlap to form a square. What is?![]() ?
?![[asy] unitsize(3mm); defaultpen(fontsize(10pt)+linewidth(.8pt)); dotfactor=4; draw((0,4)--(18,4)--(18,-4)--(0,-4)--cycle); draw((6,4)--(6,0)--(12,0)--(12,-4)); label("$A$",(0,4),NW); label("$B$",(18,4),NE); label("$C$",(18,-4),SE); label("$D$",(0,-4),SW); label("$y$",(3,4),S); label("$y$",(15,-4),N); label("$18$",(9,4),N); label("$18$",(9,-4),S); label("$8$",(0,0),W); label("$8$",(18,0),E); dot((0,4)); dot((18,4)); dot((18,-4)); dot((0,-4));[/asy]](https://latex.artofproblemsolving.com/6/6/a/66a524a2244d311dbe57cc4d9aaffc1b5e83bb03.png)
![]()
Problem 7
Mary is?![]() ?older than Sally, and Sally is?
?older than Sally, and Sally is?![]() ?younger than Danielle. The sum of their ages is?
?younger than Danielle. The sum of their ages is?![]() ?years. How old will Mary be on her next birthday?
?years. How old will Mary be on her next birthday?
![]()
Problem 8
How many sets of two or more consecutive positive integers have a sum of?![]() ?
?
![]()
Problem 9
Oscar buys?![]() ?pencils and?
?pencils and?![]() ?erasers for?
?erasers for?![]() . A pencil costs more than an eraser, and both items cost a whole number of cents. What is the total cost, in cents, of one pencil and one eraser?
. A pencil costs more than an eraser, and both items cost a whole number of cents. What is the total cost, in cents, of one pencil and one eraser?
![]()
Problem 10
For how many real values of?![]() ?is?
?is?![]() ?an integer?
?an integer?
![]()
Problem 11
Which of the following describes the graph of the equation?![]() ?
?
![]()
Problem 12
A number of linked rings, each 1 cm thick, are hanging on a peg. The top ring has an outside diameter of 20 cm. The outside diameter of each of the outer rings is 1 cm less than that of the ring above it. The bottom ring has an outside diameter of 3 cm. What is the distance, in cm, from the top of the top ring to the bottom of the bottom ring?![[asy]size(7cm); pointpen = black; pathpen = linewidth(0.7); D(CR((0,0),10)); D(CR((0,0),9.5)); D(CR((0,-18.5),9.5)); D(CR((0,-18.5),9)); MP("$vdots$",(0,-31),(0,0)); D(CR((0,-39),3)); D(CR((0,-39),2.5)); D(CR((0,-43.5),2.5)); D(CR((0,-43.5),2)); D(CR((0,-47),2)); D(CR((0,-47),1.5)); D(CR((0,-49.5),1.5)); D(CR((0,-49.5),1.0)); D((12,-10)--(12,10)); MP('20',(12,0),E); D((12,-51)--(12,-48)); MP('3',(12,-49.5),E); [/asy]](https://latex.artofproblemsolving.com/c/7/5/c7566eb2ca9233305be8873b125b5e186a871287.png)
![]()
Problem 13
The vertices of a?![]() ?right triangle are the centers of three mutually externally tangent circles,?as?shown. What is the sum of the areas of the three circles?
?right triangle are the centers of three mutually externally tangent circles,?as?shown. What is the sum of the areas of the three circles?![[asy] unitsize(5mm); defaultpen(fontsize(10pt)+linewidth(.8pt)); pair B=(0,0), C=(5,0); pair A=intersectionpoints(Circle(B,3),Circle(C,4))[0]; draw(A--B--C--cycle); draw(Circle(C,3)); draw(Circle(A,1)); draw(Circle(B,2)); label("$A$",A,N); label("$B$",B,W); label("$C$",C,E); label("3",midpoint(B--A),NW); label("4",midpoint(A--C),NE); label("5",midpoint(B--C),S);[/asy]](https://latex.artofproblemsolving.com/c/d/7/cd70a3d199aac3650e14fb5d9e5786581c4fa2ba.png)
![]()
Problem 14
Two farmers agree that pigs are worth?![]() ?dollars and that goats are worth?
?dollars and that goats are worth?![]() ?dollars. When one farmer owes the other money, he pays the debt in pigs or goats, with "change" received in the form of goats or pigs?as?necessary. (For example, a?
?dollars. When one farmer owes the other money, he pays the debt in pigs or goats, with "change" received in the form of goats or pigs?as?necessary. (For example, a?![]() ?dollar debt could be paid with two pigs, with one goat received in change.) What is the amount of the smallest positive debt that can be resolved in this way?
?dollar debt could be paid with two pigs, with one goat received in change.) What is the amount of the smallest positive debt that can be resolved in this way?
![]()
Problem 15
Suppose?![]() ?and?
?and?![]() . What is the smallest possible positive value of?
. What is the smallest possible positive value of?![]() ?
?
![]()
Problem 16
Circles with centers?![]() ?and?
?and?![]() ?have radii?
?have radii?![]() ?and?
?and?![]() , respectively. A common internal tangent intersects the circles at?
, respectively. A common internal tangent intersects the circles at?![]() ?and?
?and?![]() , respectively. Lines?
, respectively. Lines?![]() ?and?
?and?![]() ?intersect at?
?intersect at?![]() , and?
, and?![]() . What is?
. What is?![]() ?
?
![[asy]unitsize(2.5mm); defaultpen(fontsize(10pt)+linewidth(.8pt)); dotfactor=3; pair A=(0,0), Ep=(5,0), B=(5+40/3,0); pair M=midpoint(A--Ep); pair C=intersectionpoints(Circle(M,2.5),Circle(A,3))[1]; pair D=B+8*dir(180+degrees(C)); dot(A); dot(C); dot(B); dot(D); draw(C--D); draw(A--B); draw(Circle(A,3)); draw(Circle(B,8)); label("$A$",A,W); label("$B$",B,E); label("$C$",C,SE); label("$E$",Ep,SSE); label("$D$",D,NW);[/asy]](https://latex.artofproblemsolving.com/b/b/4/bb4378a1b69a2fbdd9aadc5253c2e199d58719e9.png)
![]()
Problem 17
Square?![]() ?has side length?
?has side length?![]() , a circle centered at?
, a circle centered at?![]() ?has radius?
?has radius?![]() , and?
, and?![]() ?and?
?and?![]() ?are both rational. The circle passes through?
?are both rational. The circle passes through?![]() , and?
, and?![]() ?lies on?
?lies on?![]() . Point?
. Point?![]() ?lies on the circle, on the same side of?
?lies on the circle, on the same side of?![]() ?as?
?as?![]() . Segment?
. Segment?![]() ?is tangent to the circle, and?
?is tangent to the circle, and?![]() . What is?
. What is?![]() ?
?![[asy]unitsize(6mm); defaultpen(linewidth(.8pt)+fontsize(10pt)); dotfactor=3; pair B=(0,0), C=(3,0), D=(3,3), A=(0,3); pair Ep=(3+5*sqrt(2)/6,3+5*sqrt(2)/6); pair F=intersectionpoints(Circle(A,sqrt(9+5*sqrt(2))),Circle(Ep,5/3))[0]; pair[] dots={A,B,C,D,Ep,F}; draw(A--F); draw(Circle(Ep,5/3)); draw(A--B--C--D--cycle); dot(dots); label("$A$",A,NW); label("$B$",B,SW); label("$C$",C,SE); label("$D$",D,SW); label("$E$",Ep,E); label("$F$",F,NW); [/asy]](https://latex.artofproblemsolving.com/5/0/7/5070473f4545f2932e536bc27857a5203bfe5458.png)
![]()
Problem 18
The function?![]() ?has the property that for each real number?
?has the property that for each real number?![]() ?in its domain,?
?in its domain,?![]() ?is also in its domain and
?is also in its domain and
![]()
What is the largest set of real numbers that can be in the domain of?![]() ?
?
![]() ?
?![]()
Problem 19
Circles with centers?![]() ?and?
?and?![]() ?have radii?
?have radii?![]() ?and?
?and?![]() , respectively. The equation of a common external tangent to the circles can be written in the form?
, respectively. The equation of a common external tangent to the circles can be written in the form?![]() ?with?
?with?![]() . What is?
. What is?![]() ?
?
![[asy]size(150); defaultpen(linewidth(0.7)+fontsize(8)); draw(circle((2,4),4));draw(circle((14,9),9)); draw((0,-2)--(0,20));draw((-6,0)--(25,0)); draw((2,4)--(2,4)+4*expi(pi*4.5/11)); draw((14,9)--(14,9)+9*expi(pi*6/7)); label("4",(2,4)+2*expi(pi*4.5/11),(-1,0)); label("9",(14,9)+4.5*expi(pi*6/7),(1,1)); label("(2,4)",(2,4),(0.5,-1.5));label("(14,9)",(14,9),(1,-1)); draw((-4,120*-4/119+912/119)--(11,120*11/119+912/119)); dot((2,4)^^(14,9));[/asy]](https://latex.artofproblemsolving.com/4/8/3/483a45d103ff0577c1129c68ae00f540094d6cd4.png)
![]()
Problem 20
A bug starts at one vertex of a cube and moves along the edges of the cube according to the following rule. At each vertex the bug will choose to travel along one of the three edges emanating from that vertex. Each edge has equal probability of being chosen, and all choices are independent. What is the probability that after seven moves the bug will have visited every vertex exactly once?
![]()
Problem 21
Let
![]()
and
![]() .
.
What is the ratio of the area of?![]() ?to the area of?
?to the area of?![]() ?
?
![]()
Problem 22
A circle of radius?![]() ?is concentric with and outside a regular hexagon of side length?
?is concentric with and outside a regular hexagon of side length?![]() . The probability that three entire sides of hexagon are visible from a randomly chosen point on the circle is?
. The probability that three entire sides of hexagon are visible from a randomly chosen point on the circle is?![]() . What is?
. What is?![]() ?
?
![]()
Problem 23
Given a finite sequence?![]() ?of?
?of?![]() ?real numbers, let?
?real numbers, let?![]() ?be the sequence
?be the sequence
![]()
of?![]() ?real numbers. Define?
?real numbers. Define?![]() ?and, for each integer?
?and, for each integer?![]() ,?
,?![]() , define?
, define?![]() . Suppose?
. Suppose?![]() , and let?
, and let?![]() . If?
. If?![]() , then what is?
, then what is?![]() ?
?
![]()
Problem 24
The expression
![]()
is simplified by expanding it and combining like terms. How many terms are in the simplified expression?
![]()
Problem 25
How many non-empty subsets?![]() ?of?
?of?![]() ?have the following two properties?
?have the following two properties?
![]() ?No two consecutive integers belong to?
?No two consecutive integers belong to?![]() .
.
![]() ?If?
?If?![]() ?contains?
?contains?![]() ?elements, then?
?elements, then?![]() ?contains no number less than?
?contains no number less than?![]() .
.
![]()
2006 AMC12 A 真題答案詳細解析
請掃描下方二維碼咨詢
- The?
 ?sandwiches cost?
?sandwiches cost? ?dollars. The?
?dollars. The? ?sodas cost?
?sodas cost? ?dollars. In total, the purchase costs?
?dollars. In total, the purchase costs? ?dollars. The answer is?
?dollars. The answer is? .
. - By the definition of?
 , we have?
, we have? . Then?
. Then? . The answer is?
. The answer is? .
. -
Solution 1
Let?
 ?be Mary's age. Then?
?be Mary's age. Then? . Solving for?
. Solving for? , we obtain?
, we obtain? . The answer is?
. The answer is? .
.Solution 2
We can see this is a combined ratio of?
 ,?
,? . We can equalize by doing?
. We can equalize by doing? , and?
, and? . With the common ratio of?
. With the common ratio of? ?and difference ratio of?
?and difference ratio of? , we see?
, we see? ?therefore we can see our answer is correct.
?therefore we can see our answer is correct. -
Solution 1
From the?greedy algorithm, we have?
 ?in the hours section and?
?in the hours section and? ?in the minutes section.?
?in the minutes section.?
Solution 2
With a matrix we can see?
 ?The largest digit sum we can see is?
?The largest digit sum we can see is? . For the minutes digits, we can combine the largest?
. For the minutes digits, we can combine the largest? digits, which are?
digits, which are? ?which we can then do?
?which we can then do?
- Dave and Doug paid?
 ?dollars in total. Doug paid for three slices of plain pizza, which cost?
?dollars in total. Doug paid for three slices of plain pizza, which cost? . Dave paid?
. Dave paid? ?dollars. Dave paid?
?dollars. Dave paid? ?more dollars than Doug. The answer is?
?more dollars than Doug. The answer is? .
. - Since the two?hexagons?are going to be repositioned to form a?square?without overlap, the?area?will remain the same. The rectangle's area is?
 . This means the square will have four sides of length 12. The only way to do this is shown below.
. This means the square will have four sides of length 12. The only way to do this is shown below.![[asy] size(175); pair A,B,C,D,E,F,G,H; A=(0,8); B=(12,12); C=(12,4); D=(0,0); E=(0,12); F=(12,0); G=(6,4); H=(6,8); draw(A--E--B--C--G--H--A--D--F--C); label("$A$",A,W); label("$B$",B,NE); label("$C$",(12.6,4)); label("$D$",D,SW); label("$12$",E--B,N); label("$12$",D--F,S); label("$4$",E--A,W); label("$4$",(12.4,-1.75),E); label("$8$",A--D,W); label("$8$",(12.4,4),E); label("$y$",A--H,S); label("$y$",G--C,N); [/asy]](https://latex.artofproblemsolving.com/1/7/9/1794d4dcd643f680a8bcabca8f5ff34ed2b54a70.png) As?you can see from the diagram, the?line segment?denoted?as?
As?you can see from the diagram, the?line segment?denoted?as? ?is half the length of the side of the square, which leads to?
?is half the length of the side of the square, which leads to? .
. - Let?
 ?be Mary's age, let?
?be Mary's age, let? ?be Sally's age, and let?
?be Sally's age, and let? ?be Danielle's age. We have?
?be Danielle's age. We have? , and?
, and? . The sum of their ages is?
. The sum of their ages is? . Therefore,?
. Therefore,? , and?
, and? . Then?
. Then? . Mary will be?
. Mary will be? ?on her next birthday. The answer is?
?on her next birthday. The answer is? .
. - Notice that if the consecutive positive integers have a sum of 15, then their?average?(which could be a?fraction) must be a?divisor?of 15. If the number of?integers?in the list is?odd, then the average must be either 1, 3, or 5, and 1 is clearly not possible. The other two possibilities both work:
If the number of integers in the list is even, then the average will have a?
 . The only possibility is?
. The only possibility is?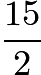 , from which we get:
, from which we get:Thus, the correct answer is 3, answer choice?
 .
. - Let the price of a pencil be?
 ?and an eraser?
?and an eraser? . Then?
. Then? ?with?
?with? . Since?
. Since? ?and?
?and? ?are?positive integers, we must have?
?are?positive integers, we must have? and?
and? .Considering the?equation?
.Considering the?equation? ?modulo?3 (that is, comparing the?remainders?when both sides are divided by 3) we have?
?modulo?3 (that is, comparing the?remainders?when both sides are divided by 3) we have? ?so?
?so? ?leaves a remainder of 1 on division by 3.Since?
?leaves a remainder of 1 on division by 3.Since? , possible values for?
, possible values for? ?are 4, 7, 10 ....Since 13 pencils cost less than 100 cents,?
?are 4, 7, 10 ....Since 13 pencils cost less than 100 cents,? .?
.? ?is too high, so?
?is too high, so? ?must be 4 or 7.If?
?must be 4 or 7.If? ?then?
?then? ?and so?
?and so? ?giving?
?giving? . This contradicts the pencil being more expensive. The only remaining value for?
. This contradicts the pencil being more expensive. The only remaining value for? ?is 7; then the 13 pencils cost?
?is 7; then the 13 pencils cost? ?cents and so the 3 erasers together cost 9 cents and each eraser costs?
?cents and so the 3 erasers together cost 9 cents and each eraser costs? ?cents.Thus one pencil plus one eraser cost?
?cents.Thus one pencil plus one eraser cost? ?cents, which is answer choice?
?cents, which is answer choice? .
. - For?
 ?to be an?integer,?
?to be an?integer,? ?must be a perfect?square.Since?
?must be a perfect?square.Since? ?can't be negative,?
?can't be negative,? .The perfect squares that are less than or equal to?
.The perfect squares that are less than or equal to? ?are?
?are? , so there are?
, so there are? ?values for?
?values for? .Since every value of?
.Since every value of? ?gives one and only one possible value for?
?gives one and only one possible value for? , the number of values of?
, the number of values of? ?is?
?is? .
. 
Either? ?or?
?or? . The?union?of them is 2 lines, and thus the answer is?
. The?union?of them is 2 lines, and thus the answer is? .
.![[asy] draw((0,-50)--(0,50));draw((-50,0)--(50,0));[/asy]](https://latex.artofproblemsolving.com/7/7/b/77bc9852606b67fe448031002c3e27a4b8a97bd1.png)
-
Solution 1
The inside diameters of the rings are the?positive integers?from 1 to 18. The total distance needed is the sum of these values plus 2 for the top of the first ring and the bottom of the last ring. Using the formula for the sum of an?arithmetic series, the answer is?
 .
.Solution 2
Alternatively, the sum of the consecutive?integers?from 3 to 20 is?
 . However, the 17?intersections?between the rings must be subtracted, and we also get?
. However, the 17?intersections?between the rings must be subtracted, and we also get? .
. - Let the radius of the smallest circle be?
 , the radius of the second largest circle be?
, the radius of the second largest circle be? , and the radius of the largest circle be?
, and the radius of the largest circle be? .
.![[r_A + r_B = 3]](https://latex.artofproblemsolving.com/d/3/2/d32fc5e73b196d772754dd22491fcd35a84bb5f3.png)
![[r_A + r_C = 4]](https://latex.artofproblemsolving.com/1/9/c/19c0750788a3a435260e2fd673e16c9ac408bd4f.png)
![[r_ B + r_C = 5]](https://latex.artofproblemsolving.com/5/b/0/5b0ea74a9c0df59da5cb769e4a8d0415e3c427ea.png) Adding up all these equations and then dividing both sides by 2, we get,
Adding up all these equations and then dividing both sides by 2, we get,![[r_A + r_B + r_C = 6]](https://latex.artofproblemsolving.com/7/d/1/7d1cefc3fb4362fcd5dbae413e070ba9c5bc3a71.png) Then, we get?
Then, we get? ,?
,? , and?
, and? ?Then we get?
?Then we get?
-
Solution 1
The problem can be restated?as?an equation of the form?
 , where?
, where? ?is the number of pigs,?
?is the number of pigs,? ?is the number of goats, and?
?is the number of goats, and? ?is the positive debt. The problem asks us to find the lowest?x?possible.?
?is the positive debt. The problem asks us to find the lowest?x?possible.? ?and?
?and? ?must be?integers, which makes the equation a?Diophantine equation. Bezout’s Identity tells us that the smallest?
?must be?integers, which makes the equation a?Diophantine equation. Bezout’s Identity tells us that the smallest? ?for the Diophantine equation?
?for the Diophantine equation? ?to have solutions is when?
?to have solutions is when? ?is the?greatest common divisor?of?
?is the?greatest common divisor?of? ?and?
?and? . Therefore, the answer is?
. Therefore, the answer is? , which is?
, which is? ,?
,?
Solution 2
Alternatively, note that?
 ?is divisible by 30 no matter what?
?is divisible by 30 no matter what? ?and?
?and? ?are, so our answer must be divisible by 30. In addition, three goats minus two pigs gives us?
?are, so our answer must be divisible by 30. In addition, three goats minus two pigs gives us? ?exactly. Since our theoretical best can be achieved, it must really be the best, and the answer is?
?exactly. Since our theoretical best can be achieved, it must really be the best, and the answer is? . debt that can be resolved.
. debt that can be resolved.Solution 3
Let us simplify this problem. Dividing by?
 , we get a pig to be:?
, we get a pig to be:? , and a goat to be?
, and a goat to be? . It becomes evident that if you exchange?
. It becomes evident that if you exchange? pigs for?
pigs for? ?goats, we get the smallest positive difference -?
?goats, we get the smallest positive difference -? . Since we originally divided by?
. Since we originally divided by? , we need to multiply again, thus getting the answer:?
, we need to multiply again, thus getting the answer:?
- For?
 , x must be in the form of?
, x must be in the form of? , where?
, where? ?denotes any?integer.
?denotes any?integer. - For?
 ,?
,? .
.
- For?
- The smallest possible value of?
 ?will be that of?
?will be that of? .
. 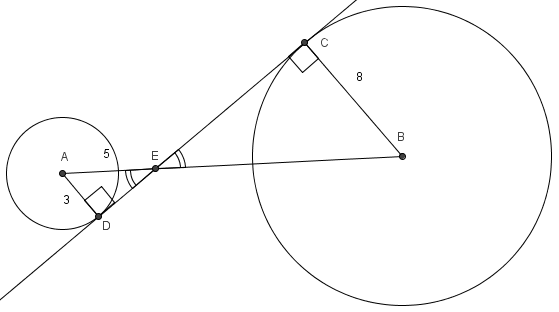
 ?and?
?and? ?are vertical angles so they are?congruent,?as?are?angles?
?are vertical angles so they are?congruent,?as?are?angles? ?and?
?and? ?(both are?right angles?because the radius and?tangent line?at a point on a circle are always?perpendicular). Thus,?
?(both are?right angles?because the radius and?tangent line?at a point on a circle are always?perpendicular). Thus,? . By the?Pythagorean Theorem,?line segment?
. By the?Pythagorean Theorem,?line segment? . The sides are?proportional, so?
. The sides are?proportional, so? . This makes?
. This makes? ?and?
?and? .
.-
Solution 1
One possibility is to use the?coordinate plane, setting?
 ?at the origin. Point?
?at the origin. Point? ?will be?
?will be? ?and?
?and? ?will be?
?will be? ?since?
?since? , and?
, and? ?are?collinear?and contain a diagonal of?
?are?collinear?and contain a diagonal of? . The?Pythagorean theorem?results in
. The?Pythagorean theorem?results in![[AF^2 + EF^2 = AE^2]](https://latex.artofproblemsolving.com/d/7/1/d71803837ddd2739fca2601339696a8bda7a977c.png)
![[r^2 + left(sqrt{9 + 5sqrt{2}}right)^2 = left(left(s + frac{r}{sqrt{2}}right) - 0right)^2 + left(left(s + frac{r}{sqrt{2}}right) - sright)^2]](https://latex.artofproblemsolving.com/5/f/d/5fdeb0d443078117c60e8fd7a8bc11fac819921d.png)
![[r^2 + 9 + 5sqrt{2} = s^2 + rssqrt{2} + frac{r^2}{2} + frac{r^2}{2}]](https://latex.artofproblemsolving.com/5/0/3/5035fb6846965c9f72d4bab118a4348594b3539d.png)
![[9 + 5sqrt{2} = s^2 + rssqrt{2}]](https://latex.artofproblemsolving.com/d/4/c/d4c51cc1cc2c9c1a9f1289b458925ff8757c55b9.png)
This implies that?
 ?and?
?and? ; dividing gives us?
; dividing gives us? .
.Solution 2
First note that angle?
 ?is right since?
?is right since? ?is tangent to the circle. Using the Pythagorean Theorem on?
?is tangent to the circle. Using the Pythagorean Theorem on? , then, we see
, then, we see![[AE^2 = 9 + 5sqrt{2} + r^2.]](https://latex.artofproblemsolving.com/2/5/c/25c4083d528c34ad1d6367510a4e14faccac95f1.png)
But it can also be seen that?
 . Therefore, since?
. Therefore, since? ?lies on?
?lies on? ,?
,? . Using the Law of Cosines on?
. Using the Law of Cosines on? , we see
, we see![[AE^2 = s^2 + r^2 - 2srcos(135^circ)]](https://latex.artofproblemsolving.com/8/1/6/8161db3710ab9fa2497d6e595aa9b77859ca1577.png)
![[AE^2 = s^2 + r^2 - 2srleft(-frac{1}{sqrt{2}}right)]](https://latex.artofproblemsolving.com/e/c/a/eca29b32ce59ee360a954cac585dbdfeee4c25b9.png)
![[AE^2 = s^2 + r^2 + sqrt{2}sr]](https://latex.artofproblemsolving.com/4/0/5/40563b86e4b5862175b46ba601c2357078403ecc.png)
![[9 + 5sqrt{2} + r^2 = s^2 + r^2 + sqrt{2}sr]](https://latex.artofproblemsolving.com/9/a/b/9ab7aedd4738e7284f627b50809732dacad3f1c6.png)
![[9 + 5sqrt{2} = s^2 + sqrt{2}sr.]](https://latex.artofproblemsolving.com/c/e/b/ceb83cd257547b0822adade5376c7986adb35db7.png)
Thus, since?
 ?and?
?and? ?are rational,?
?are rational,? ?and?
?and? . So?
. So? ,?
,? , and?
, and? .
.Solution 3
(Similar to Solution 1) First, draw line AE and mark a point Z that is equidistant from E and D so that?
 ?and that line?
?and that line? ?includes point D. Since DE is equal to the radius?
?includes point D. Since DE is equal to the radius? ,?
,?
Note that triangles?
 ?and?
?and? ?share the same hypotenuse?
?share the same hypotenuse? , meaning that
, meaning that![[AZ^2+EZ^2=AF^2+EF^2]](https://latex.artofproblemsolving.com/f/6/6/f663e70afe26fee9429f9c29f2033a144f67731b.png) Plugging in our values we have:
Plugging in our values we have:![[(s+frac{rsqrt{2}}{2})^2+(frac{rsqrt{2}}{2})^2=(sqrt{9+5sqrt{2}})^2+r^2]](https://latex.artofproblemsolving.com/b/9/a/b9a65652c1aafc775a78f65420d00204260e7ea4.png)
![[s^2+srsqrt{2}+frac{r^2}{2}+frac{r^2}{2}=9+5sqrt{2}+r^2]](https://latex.artofproblemsolving.com/e/f/5/ef5e6ee171a750a306c118b67f27c3cf96e32dda.png)
![[s^2+srsqrt{2}=9+5sqrt{2}]](https://latex.artofproblemsolving.com/5/6/4/5640b3c27003030cc9bc0dd605220ee494b14993.png) By logic?
By logic? ?and?
?and?
Therefore,?

- Quickly verifying by plugging in values verifies that?
 ?and?
?and? ?are in the domain.
?are in the domain. Plugging in?
Plugging in? ?into the?function:
?into the?function:
 Since?
Since? ?cannot have two values:
?cannot have two values:


Therefore, the largest?set?of?real numbers?that can be in the?domain?of?
 ?is
?is 
- Let?
 ?be the line that goes through?
?be the line that goes through? ?and?
?and? , and let?
, and let? ?be the line?
?be the line? . If we let?
. If we let? ?be the measure of the acute angle formed by?
?be the measure of the acute angle formed by? ?and the x-axis, then?
?and the x-axis, then? .?
.? ?clearly bisects the angle formed by?
?clearly bisects the angle formed by? ?and the x-axis, so?
?and the x-axis, so? . We also know that?
. We also know that? ?and?
?and? ?intersect at a point on the x-axis. The equation of?
?intersect at a point on the x-axis. The equation of? ?is?
?is? , so the coordinate of this point is?
, so the coordinate of this point is? . Hence the equation of?
. Hence the equation of? ?is?
?is? , so?
, so? , and our answer choice is?
, and our answer choice is? .
. -
Solution 1
![[asy] import three; unitsize(1cm); size(50); currentprojection=orthographic(1/2,-1,1/2); /* three - currentprojection, orthographic */ draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle); draw((0,0,0)--(0,0,1)); draw((0,1,0)--(0,1,1)); draw((1,1,0)--(1,1,1)); draw((1,0,0)--(1,0,1)); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle); [/asy]](https://latex.artofproblemsolving.com/0/c/3/0c387d5337e7fcb06d2997018524c80f0caef086.png)
Let us count the good paths. The bug starts at an arbitrary?vertex, moves to a neighboring vertex (3 ways), and then to a new neighbor (2 more ways). So,?without loss of generality, let the?cube?have vertices?
 ?such that?
?such that? ?and?
?and? ?are two opposite?faces?with?
?are two opposite?faces?with? above?
above? ?and?
?and? ?above?
?above? . The bug starts at?
. The bug starts at? ?and moves first to?
?and moves first to? , then to?
, then to? .
.From this point, there are two?cases.
Case 1: the bug moves to?
 . From?
. From? , there is only one good move available, to?
, there is only one good move available, to? . From?
. From? , there are two ways to finish the trip, either by going?
, there are two ways to finish the trip, either by going? ?or?
?or? . So there are 2 good paths in this case.
. So there are 2 good paths in this case.Case 2: the bug moves to?
 . Case 2a: the bug moves?
. Case 2a: the bug moves? . In this case, there are 0 good paths because it will not be possible to visit both?
. In this case, there are 0 good paths because it will not be possible to visit both? ?and?
?and? ?without double-visiting some vertex. Case 2b: the bug moves?
?without double-visiting some vertex. Case 2b: the bug moves? . There is a unique good path in this case,?
. There is a unique good path in this case,? .
.Thus, all told we have 3 good paths after the first two mo, for a total of?
 ?good paths. There were?
?good paths. There were? ?possible paths the bug could have taken, so the?probability?a random path is good is the?ratio?of good paths to total paths,?
?possible paths the bug could have taken, so the?probability?a random path is good is the?ratio?of good paths to total paths,? .
.Solution 2 (using the answer choices)
As?in Solution 1, the bug can move from its arbitrary starting vertex to a neighboring vertex in 3 ways. After this, the bug can move to a new neighbor in 2 ways (it cannot return to the first vertex). The total number of paths (as?stated above) is?
 ?or?
?or? . Therefore, the probability of the bug following a good path is equal to?
. Therefore, the probability of the bug following a good path is equal to? ?for some positive integer?
?for some positive integer? . The only answer choice which can be expressed in this form is?
. The only answer choice which can be expressed in this form is? .
. - Looking at the constraints of?
 :
:






 ?is a circle with a radius of?
?is a circle with a radius of? . So, the area of?
. So, the area of? ?is?
?is? .
.Looking at the constraints of?
 :
:






 ?is a circle with a radius of?
?is a circle with a radius of? . So, the area of?
. So, the area of? ?is?
?is? .
.So the desired ratio is?
 .
. - Project any two non-adjacent and non-opposite sides of the?hexagon?to the?circle; the?arc?between the two points formed is the location where all three sides of the hexagon can be fully viewed. Since there are six such pairs of sides, there are six arcs. The probability of choosing a point is?
 , or if the total arc degree measures add up to?
, or if the total arc degree measures add up to? . Each arc must equal?
. Each arc must equal? .
.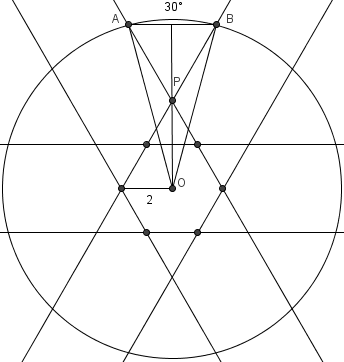 Call the center?
Call the center? , and the two endpoints of the arc?
, and the two endpoints of the arc? ?and?
?and? , so?
, so? . Let?
. Let? ?be the intersections of the projections of the sides of the hexagon corresponding to?
?be the intersections of the projections of the sides of the hexagon corresponding to? . Notice that?
. Notice that? ?is an?isosceles triangle:?
?is an?isosceles triangle:? ?and?
?and? . Since?
. Since? ?is a radius and?
?is a radius and? ?can be found in terms of a side of the hexagon, we are almost done.If we draw the altitude of?
?can be found in terms of a side of the hexagon, we are almost done.If we draw the altitude of? ?from?
?from? , then we get a?right triangle. Using simple trigonometry,?
, then we get a?right triangle. Using simple trigonometry,? .Since?
.Since? , we get?
, we get? .
.  ?
? ?
? In general,?
In general,? ?such that?
?such that? ?has?
?has? ?terms. Specifically,?
?terms. Specifically,? ?To find x, we need only solve the equation?
?To find x, we need only solve the equation? . Algebra yields?
. Algebra yields? .
.-
Solution 1
By the?Multinomial Theorem, the summands can be written?as
![[sum_{a+b+c=2006}{frac{2006!}{a!b!c!}x^ay^bz^c}]](https://latex.artofproblemsolving.com/7/b/7/7b78526602fd2bf277218a45fd8d1fdcc3efcdf4.png)
and
![[sum_{a+b+c=2006}{frac{2006!}{a!b!c!}x^a(-y)^b(-z)^c},]](https://latex.artofproblemsolving.com/1/3/5/1353e7455d59a32ac3de47ace211b252a9bd0cf6.png)
respectively. Since the coefficients of like terms are the same in each expression, each like term either cancel one another out or the coefficient doubles. In each expansion there are:
![[{2006+2choose 2} = 2015028]](https://latex.artofproblemsolving.com/8/d/3/8d3ff6f9a5045933c1619fcab5e8bd4a48ee0457.png)
terms without cancellation. For any term in the second expansion to be negative, the parity of the exponents of?
 ?and?
?and? ?must be opposite. Now we find a pattern:
?must be opposite. Now we find a pattern:if the exponent of?
 ?is 1, the exponent of?
?is 1, the exponent of? ?can be all even integers up to 2004, so there are 1003 terms.
?can be all even integers up to 2004, so there are 1003 terms.if the exponent of?
 ?is 3, the exponent of?
?is 3, the exponent of? ?can go up to 2002, so there are 1002 terms.
?can go up to 2002, so there are 1002 terms.
if the exponent of?
 ?is 2005, then?
?is 2005, then? ?can only be 0, so there is 1 term.
?can only be 0, so there is 1 term.If we add them up, we get?
 ?terms. However, we can switch the exponents of?
?terms. However, we can switch the exponents of? ?and?
?and? ?and these terms will still have a negative sign. So there are a total of?
?and these terms will still have a negative sign. So there are a total of? ?negative terms.
?negative terms.By subtracting this number from 2015028, we obtain?
 ?or?
?or? ?as?our answer.
?as?our answer.Solution 2
Alternatively, we can use a?generating function?to solve this problem. The goal is to find the generating function for the number of unique terms in the simplified expression (in terms of?
 ). In other words, we want to find?
). In other words, we want to find? ?where the coefficient of?
?where the coefficient of? ?equals the number of unique terms in?
?equals the number of unique terms in? .
.First, we note that all unique terms in the expression have the form,?
 , where?
, where? ?and?
?and? ?is some constant. Therefore, the generating function for the MAXIMUM number of unique terms possible in the simplified expression of?
?is some constant. Therefore, the generating function for the MAXIMUM number of unique terms possible in the simplified expression of? ?is
?is![[(1+x+x^2+x^3cdots)^3 = frac{1}{(1-x)^3}]](https://latex.artofproblemsolving.com/8/4/c/84c7d0006cfd2e05e461469355b98a403024b42c.png)
Secondly, we note that a certain number of terms of the form,?
 , do not appear in the simplified version of our expression because those terms cancel. Specifically, we observe that terms cancel when?
, do not appear in the simplified version of our expression because those terms cancel. Specifically, we observe that terms cancel when? ?because every unique term is of the form:
?because every unique term is of the form:![[binom{k}{a,b,c}x^ay^bz^c+(-1)^{b+c}binom{k}{a,b,c}x^ay^bz^c]](https://latex.artofproblemsolving.com/4/3/9/439e76ff20585a54ea8ac17bcc0f8263e4c81b56.png) for all possible?
for all possible? .
.Since the generating function for the maximum number of unique terms is already known, it is logical that we want to find the generating function for the number of terms that cancel, also in terms of?
 . With some thought, we see that this desired generating function is the following:
. With some thought, we see that this desired generating function is the following:![[2(x+x^3+x^5cdots)(1+x^2+x^4cdots)(1+x+x^2+x^3cdots) = frac{2x}{(1-x)^3(1+x)^2}]](https://latex.artofproblemsolving.com/e/e/6/ee6d5ceef465fdd6d7a1cb47f3c8363ae8b28f26.png)
Now, we want to subtract the latter from the former in order to get the generating function for the number of unique terms in?
 , our initial goal:
, our initial goal:![[frac{1}{(1-x)^3}-frac{2x}{(1-x)^3(1+x)^2} = frac{x^2+1}{(1-x)^3(1+x)^2}]](https://latex.artofproblemsolving.com/9/1/b/91b72d34758e7ed145a1c511bd2723978d2439a4.png) which equals
which equals![[(x^2+1)(1+x+x^2cdots)^3(1-x+x^2-x^3cdots)^2]](https://latex.artofproblemsolving.com/3/0/f/30f0bb48c16a88abe79887795d4c9a4cb7a2724c.png)
The coefficient of?
 ?of the above expression equals
?of the above expression equals![[sum_{a=0}^{2006}binom{2+a}{2}binom{1+2006-a}{1}(-1)^a + sum_{a=0}^{2004}binom{2+a}{2}binom{1+2004-a}{1}(-1)^a]](https://latex.artofproblemsolving.com/6/5/6/656d32098986fa900dc1f04828eb37888180a9bc.png)
Evaluating the expression, we get?
 ,?as?expected.
,?as?expected.Solution 3
Define?
 ?such that?
?such that? . Then the expression in the problem becomes:?
. Then the expression in the problem becomes:? .
.Expanding this using binomial theorem gives?
 , where?
, where? ?(we may omit the coefficients,?as?we are seeking for the number of terms, not the terms themselves).
?(we may omit the coefficients,?as?we are seeking for the number of terms, not the terms themselves).Simplifying gives:?
 . Note that two terms that come out of different powers of?
. Note that two terms that come out of different powers of? ?cannot combine and simplify,?as?their exponent of?
?cannot combine and simplify,?as?their exponent of? ?will differ. Therefore, we simply add the number of terms produced from each addend. By the Binomial Theorem,?
?will differ. Therefore, we simply add the number of terms produced from each addend. By the Binomial Theorem,? ?will have?
?will have? ?terms, so the answer is?
?terms, so the answer is? .
.Solution 4
Using stars and bars we know that?
 ?has?
?has? ?or?
?or? ?different terms. Now we need to find out how many of these terms are canceled out by?
?different terms. Now we need to find out how many of these terms are canceled out by? . We know that for any term(let's say?
. We know that for any term(let's say? ) where?
) where? ?of the expansion of
?of the expansion of ?is only going to cancel out with the corresponding term?
?is only going to cancel out with the corresponding term? ?if only?
?if only? ?is odd and?
?is odd and? ?is even or?
?is even or? ?is even and?
?is even and? ?is odd. Now let's do some casework to see how many terms fit this criteria:
?is odd. Now let's do some casework to see how many terms fit this criteria:Case 1:?
 ?is even
?is evenNow we know that?
 ?is even and?
?is even and? . Thus?
. Thus? ?is also even or both?
?is also even or both? ?and?
?and? ?are odd or both?
?are odd or both? ?and?
?and? ?are even. This case clearly fails the above criteria and there are 0 possible solutions.
?are even. This case clearly fails the above criteria and there are 0 possible solutions.Case 2:?
 ?is odd
?is oddNow we know that?
 ?is odd and?
?is odd and? . Thus?
. Thus? ?is odd and?
?is odd and? ?is odd and?
?is odd and? ?is even or?
?is even or? ?is even and?
?is even and? ?is odd. All terms that have?
?is odd. All terms that have? being odd work.
being odd work.We now need to figure out how many of the terms have?
 ?as?a odd number. We know that?
?as?a odd number. We know that? ?can be equal to any number between 0 and 2006. There are 1003 odd numbers between this range and 2007 total numbers. Thus?
?can be equal to any number between 0 and 2006. There are 1003 odd numbers between this range and 2007 total numbers. Thus? ?of the?
?of the? ?terms will cancel out and?
?terms will cancel out and? ?of the terms will work. Thus there are?
?of the terms will work. Thus there are? ?terms. This number comes out to be?
?terms. This number comes out to be? ?
? ?(Author: David Camacho)
?(Author: David Camacho) -
Solution 1
This question can be solved fairly directly by casework and pattern-finding. We give a somewhat more general attack, based on the solution to the following problem:
How many ways are there to choose?
 ?elements from an ordered?
?elements from an ordered? ?element?set?without choosing two consecutive members?
?element?set?without choosing two consecutive members?You want to choose?
 ?numbers out of?
?numbers out of? ?with no consecutive numbers. For each configuration, we can subtract?
?with no consecutive numbers. For each configuration, we can subtract? ?from the?
?from the? -th element in your subset. This converts your configuration into a configuration with?
-th element in your subset. This converts your configuration into a configuration with? ?elements where the largest possible element is?
?elements where the largest possible element is? , with no restriction on consecutive numbers. Since this process is easily reversible, we have a?bijection. Without consideration of the second condition, we have:?
, with no restriction on consecutive numbers. Since this process is easily reversible, we have a?bijection. Without consideration of the second condition, we have:?
Now we examine the second condition. It simply states that no element in our original configuration (and hence also the modified configuration, since we don't move the smallest element) can be less than?
 , which translates to subtracting?
, which translates to subtracting? ?from the "top" of each?binomial coefficient. Now we have, after we cancel all the terms?
?from the "top" of each?binomial coefficient. Now we have, after we cancel all the terms? ?where?
?where? ,
,
Solution 2
Another way of visualizing the solution above would be to use?
 's and?
's and? 's. Denote?
's. Denote? ?as?the numbers we have chosen and?
?as?the numbers we have chosen and? ?as?other numbers. Taking an example, assuming we are picking two numbers, we imagine the shape?
?as?other numbers. Taking an example, assuming we are picking two numbers, we imagine the shape? . This notation forces a number between the two chosen numbers, which blocks the two numbers we picked from being consecutive. Now we consider the orientations with this shape. We have?
. This notation forces a number between the two chosen numbers, which blocks the two numbers we picked from being consecutive. Now we consider the orientations with this shape. We have? ?remaining numbers.
?remaining numbers.We need to find the number of ways to place the remaining?
 's. We can find this by utilizing stars and bars, with the following marker being placed to represent groups: *| - *|*. Now, we have to place?
's. We can find this by utilizing stars and bars, with the following marker being placed to represent groups: *| - *|*. Now, we have to place? ?numbers within?
?numbers within? ?groups, which is?
?groups, which is? . The same concept can be used for the remaining numbers. The rest of the solution continues?as?above.
. The same concept can be used for the remaining numbers. The rest of the solution continues?as?above.Solution by: Everyoneintexas
Solution 3
We have the same setup?as?in the previous solution.
Note that if?
 , the answer will be 0. Otherwise, the?
, the answer will be 0. Otherwise, the? ?elements we choose define?
?elements we choose define? ?boxes (which divide the nonconsecutive numbers) into which we can drop the?
?boxes (which divide the nonconsecutive numbers) into which we can drop the? ?remaining elements, with the caveat that each of the middle?
?remaining elements, with the caveat that each of the middle? ?boxes must have at least one element (since the numbers are nonconsecutive). This is equivalent to dropping?
?boxes must have at least one element (since the numbers are nonconsecutive). This is equivalent to dropping? ?elements into?
?elements into? ?boxes, where each box is allowed to be empty. And this is equivalent to arranging?
?boxes, where each box is allowed to be empty. And this is equivalent to arranging? ?objects,?
?objects,? ?of which are dividers, which we can do in?
?of which are dividers, which we can do in? ?ways.
?ways.Now, looking at our original question, we see that the thing we want to calculate is just?

以上解析方式僅供參考

最新發(fā)布
? 2025. All Rights Reserved. 滬ICP備2023009024號-1









