中考數學幾何重難點：矩形相關知識內容以及題型講解分析

 

矩形是初中幾何內容中最重要、最常見的內容之一，歷年大部分與幾何有關的中考試題，多多少少都會牽涉到矩形的知識內容。因此，大家無論是在平時數學學習階段，還是中考復習沖刺階段，都要認真對待矩形內容的學習。

什么是矩形？

我們把有一個角是直角的平行四邊形叫做矩形。

從矩形的概念進行分析，我們可以把正方形和長方形看成是矩形兩種特殊形態。這也就說明了矩形除了具有平行四邊形的性質之外，還有具有自己一些特有的性質，如：

1、矩形的四個角都是直角

2、矩形的對角線相等

3、矩形是軸對稱圖形

中考數學，矩形，典型例題分析1：

已知：如圖所示的一張矩形紙片ABCD（AD>AB），將紙片折疊一次，使點A與點C重合，再展開，折痕EF交AD邊于點E，交BC邊于點F，分別連結AF和CE。

（1）求證：四邊形AFCE是菱形；

（2）若AE=10cm，△ABF的面積為24cm2，求△ABF的周長；

（3）在線段AC上是否存在一點P，使得2AE2=AC·AP？若存在，請說明點P的位置，并予以證明；若不存在，請說明理由.

證明：（1）由題意可知OA=OC，EF⊥AO，

∵AD∥BC，

∴∠AEO=∠CFO，∠EAO=∠FCO，

∴△AOE≌△COF，

∴AE=CF，又AE∥CF，

∴四邊形AECF是平行四邊形，

∵AC⊥EF，

∴四邊形AECF是菱形；

（2）∵四邊形AECF是菱形，

∴AF=AE=10cm，

設AB=a，BF=b，

∵△ABF的面積為24cm2，

∴a2+b2=100，ab=48，

∴（a+b）2=196，

∴a+b=14或a+b=﹣14（不合題意，舍去），

∴△ABF的周長為14+10=24cm；

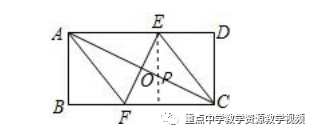
（3）存在，過點E作AD的垂線，交AC于點P，

點P就是符合條件的點；

∵∠AEP=∠AOE=90°，∠EAO=∠EAP，

∴△AOE∽△AEP，

∴AE/AP=AO/AE，

∴AE2=AO?AP，

∵四邊形AECF是菱形，

∴AO=AC/2，

∴AE2=AC?AP/2，

∴2AE2=AC?AP．

考點分析：

相似三角形的判定與性質；全等三角形的判定與性質；勾股定理；矩形的性質；翻折變換（折疊問題）.

題干分析：

（1）通過證明△AOE≌△COF，可得四邊形AFCE是平行四邊形；由折疊的性質，可得AE=EC，即可證明；

（2）由勾股定理得AB2+FB2=100，△ABF的面積為24cm2可得，AB×BF=48；變換成完全平方式，即可解答；

（3）過點E作AD的垂線，交AC于點P，通過證明△AOE∽△AEP，即可證明；

解題反思：

本題考查了相似和全等三角形的判定和性質、勾股定理及矩形的性質，考查了知識點較多，綜合性較強，考查了學生綜合運用所學知識解決問題的能力。

我們如何才能判斷一個四邊形是不是矩形？要記住以下三個判定方法：

1、定義：有一個角是直角的平行四邊形是矩形；

2、定理1：有三個角是直角的四邊形是矩形；

3、定理2：對角線相等的平行四邊形是矩形；