AMC10/12試題分析之2008AMC12A25數列與矩陣

[vc_btn title="2021 AMC10/AMC12 報名" style="classic" color="primary" size="lg" align="center" link="url:https%3A%2F%2Fjinshuju.net%2Ff%2FXq7Rke%3Fx_field_1%3Dweb||target:%20_blank|rel:nofollow"]

2008AMC12A25數列與矩陣

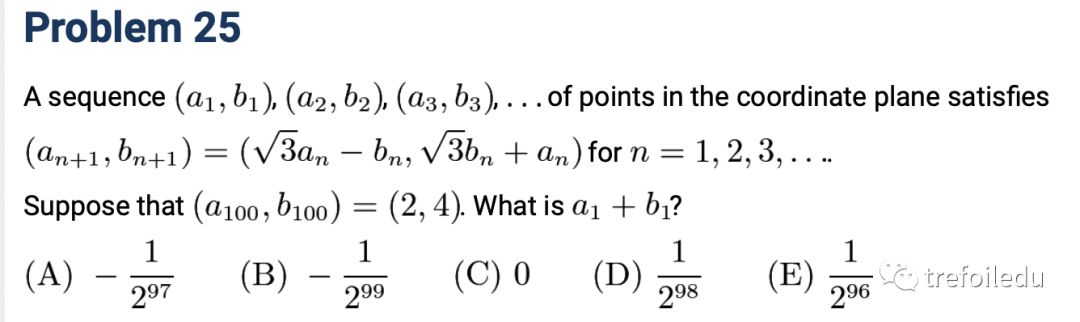
題目用遞推關系定義了一個序列，我們先來理解這個遞推關系：

由(1)易知：

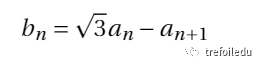
將(2)代入(1)，得：

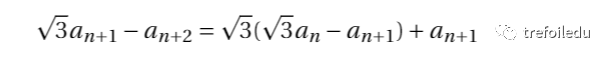
化簡得到：

由(2)得：

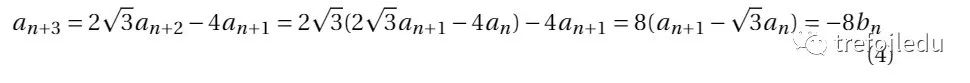
同理，

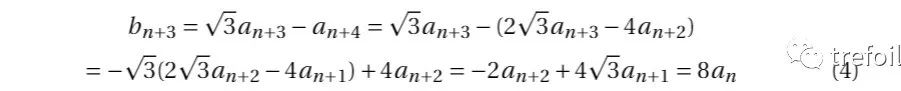
因此，

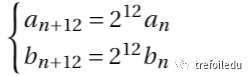
所以：

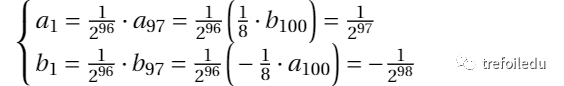
所以：

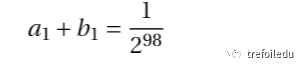
故選D.

我們都知道，很多AMC的學術活動題有這樣的特點：如果僅借助現階段的知識體系，往往解法很繁瑣。這是因為這類題目往往來自高等數學知識點的前置，如果掌握了該前置的知識點，就能得到出人意料的簡潔解法。以這道題目為基礎，我們希望一起感受矩陣的妙用。

首先，請大家觀察遞推關系：

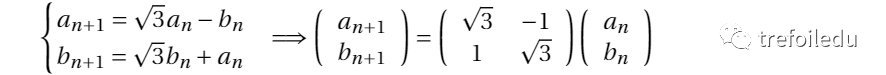
我們發現，該遞推關系可以用一個2*2矩陣來表示，而且每個2*2矩陣與??到??的線性變換一一對應。由于逆時針旋轉?角對應的矩陣為：

因此，順時針旋轉?角對應的矩陣為：

因此，逆時針旋轉度角對應的矩陣為：

在這種觀點下，我們發現題目中給出的遞推關系的矩陣可表示為：

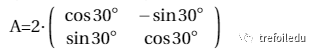
因此，

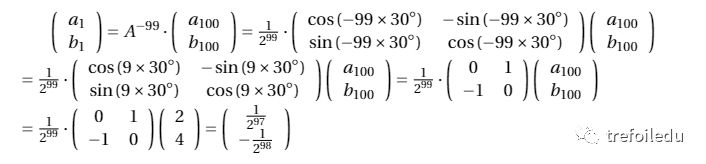
至此，我們把一個看似很復雜的數列問題轉化成線性變換的問題，然后用矩陣的工具加以解決，避免了繁雜的運算。經過這個例子，我們得以一窺矩陣的作用。本題中，我們用到了線性變換與矩陣的一一對應關系，實際上，對這一問題，數學家們有更深入的認識，例如，可逆線性變換與可逆矩陣的一一對應關系，進一步的，可逆線性變換的全體構成一個群，我們稱之為一般線性變換群。而一般線性變換群是群論表示理論以及代數學中至關重要的一個工具，數學家們用它去刻畫各種群變換的表示，以及給各種重要的代數做分類。