Edexcel A Level Further Maths: Core Pure:復習筆記1.2.1 Exponential Form
Exponential Form
You now know how to do lots of operations with complex numbers: add, subtract, multiply, divide, raise to a power and even square root. The last operation to learn is raising the number e to the power of an imaginary number.
How do we calculate e to the power of an imaginary number?
- Given an imaginary number (iθ) we can?define exponentiation?as
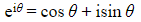
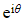is the complex number with modulus 1 and argument θ
- This works with our current rules of exponents
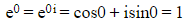
- This shows e to the power 0 would still give the answer of 1
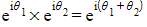
- This is because when you?multiply complex numbers?you can?add?the?arguments
- This shows that when you multiply two powers you can still add the indices
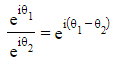
- This is because when you?divide complex numbers?you can?subtract?the?arguments
- This shows that when you divide two powers you can still subtract the indices
What is the exponential form of a complex number?
- Any complex number
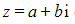?can be written in?polar form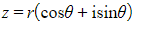 
- r?is the modulus
- θ?is the argument
- Using the definition of 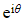we can now also write
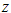?in?exponential form
Why do I need to use the exponential form of a complex number?
- It's just a?shorter?and?quicker?way of expressing complex numbers
- It makes a link between the?exponential function?and?trigonometric functions
- It makes it easier to remember what happens with the moduli and arguments when multiplying and dividing
What are some common numbers in exponential form?
- As
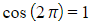?and 
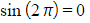?you can write:
- Using the same idea you can write:
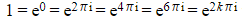where k?is any integer
- As
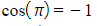and 
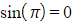?you can write:
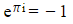
- Or more commonly written as
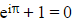
- As
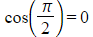?and 
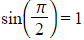?you can write:
Exam Tip
- The powers can be long and contain fractions so make sure you write the expression clearly.
- You don’t want to lose marks because the examiner can’t read your answer
Worked Example
Two complex numbers are given by 
?and 
.
a) Write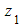 
?in the form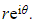 
?in the form 
b) Write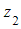 
?in?the form 
.
?in?the form .
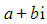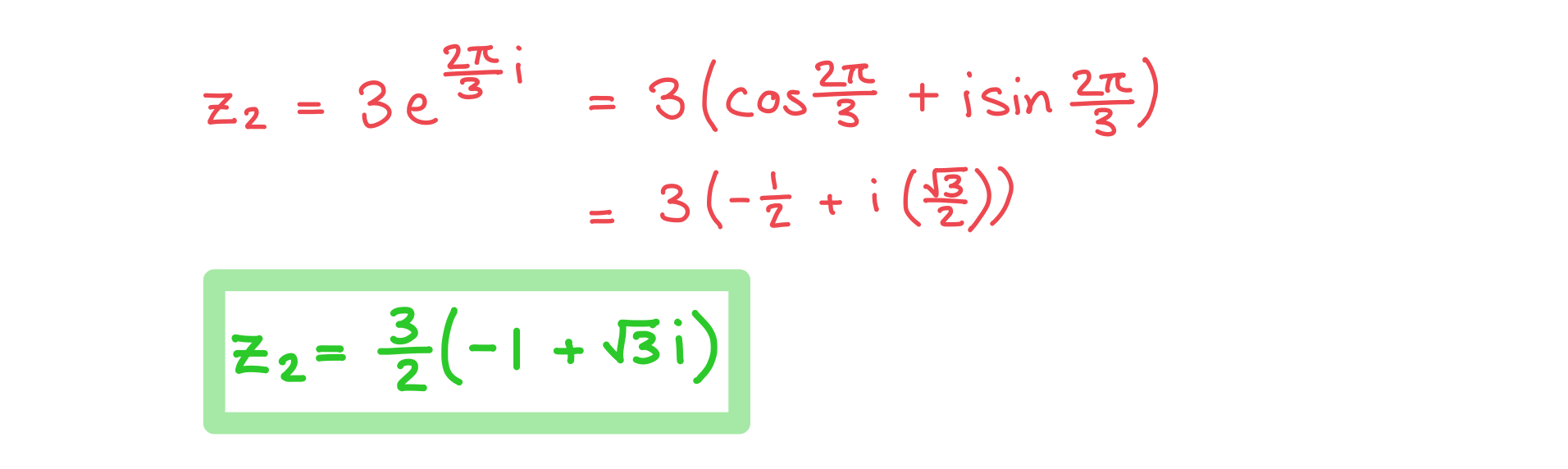
Operations using Exponential Form
How do I multiply and divide exponential forms of complex numbers?
- If
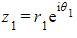?and 
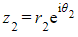?then
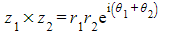
- You can clearly see that the?moduli have been multiplied?and the?arguments have been added
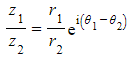
- You can clearly see that the?moduli have been divided?and the?arguments have been subtracted
How do I find the complex conjugate of a complex number in exponential form?
- Simply change the sign of the argument(s)
- If
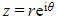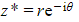
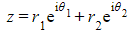?then 
then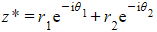 
- If
Worked Example
Consider the complex number 
. Calculate 
?giving your answer in the form 
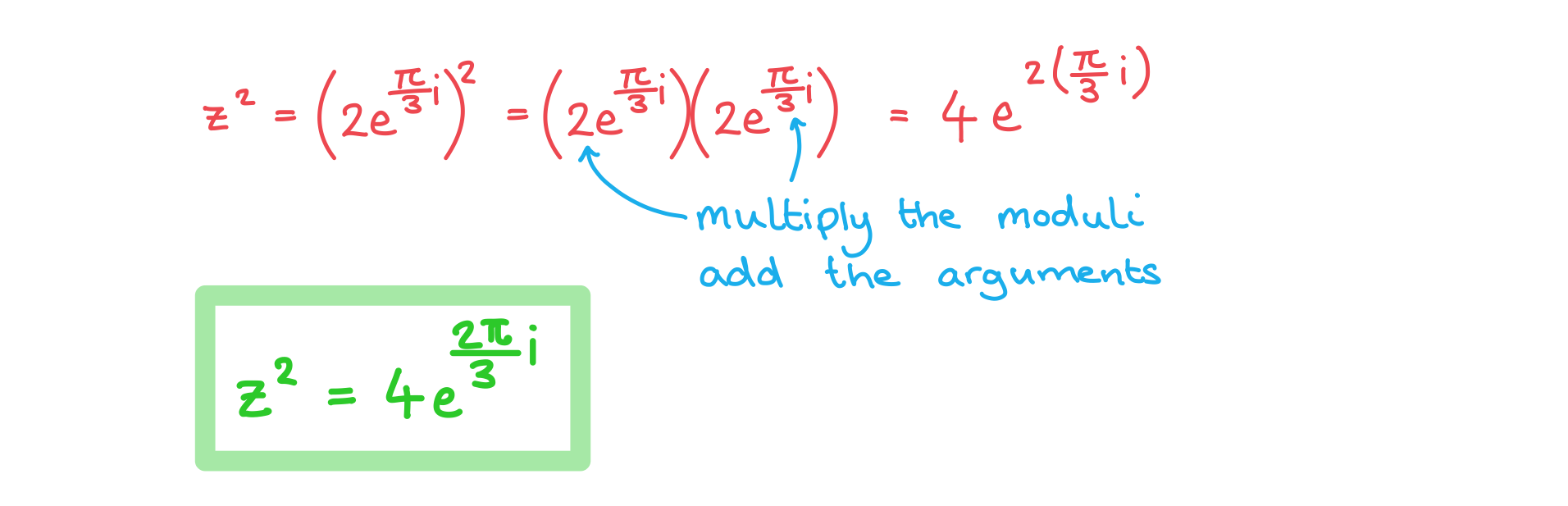
轉載自savemyexams
國際競賽真題資源免費領取
美高學分項目重磅來襲！立即了解
