- 翰林提供學術活動、國際課程、科研項目一站式留學背景提升服務!
- 400 888 0080
Edexcel A Level Physics:復習筆記5.9 Stationary Waves
Stationary Waves
- Stationary waves, or standing waves, are produced by the?superposition?of two waves of the?same frequency?and?amplitude?travelling in?opposite directions
- This is usually achieved by a travelling wave and its?reflection. The superposition produces a wave pattern where the?peaks?and?troughs?do not move
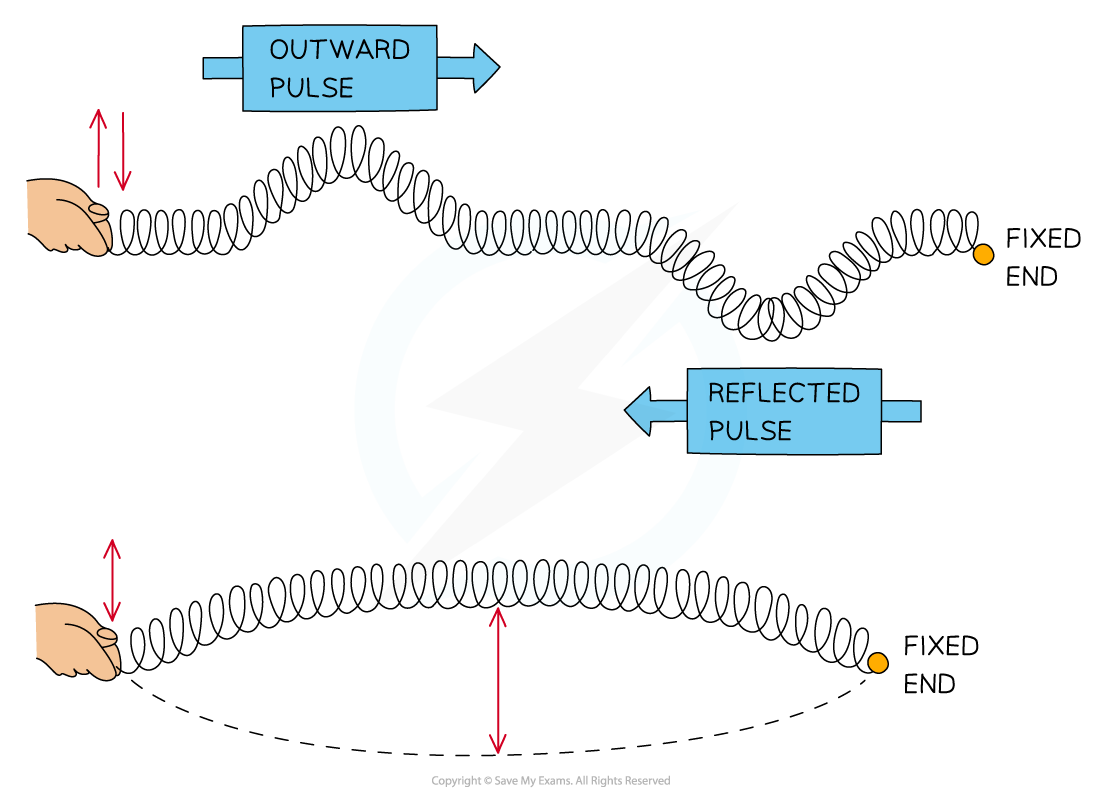
Formation of a stationary wave on a stretched spring fixed at one end
- In this section, we will look at a few experiments that demonstrate stationary waves in everyday life
Stretched Strings
- Vibrations caused by stationary waves on a stretched string produce sound
- This is how stringed instruments, such as guitars or violins, work
- This can be demonstrated by an oscillator vibrating a length of string under tension fixed at one end:
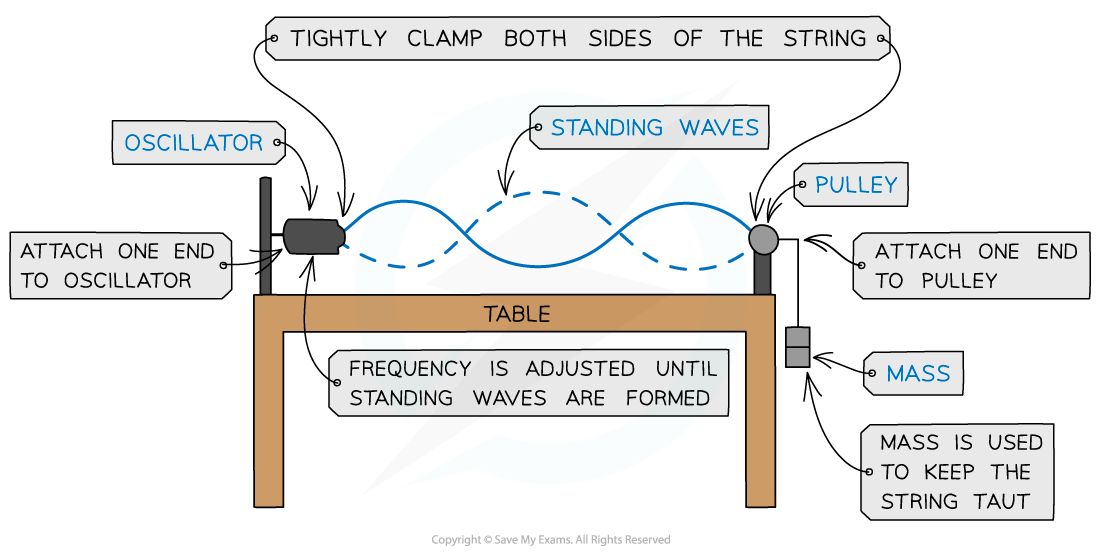
Stationary wave on a stretched string
- As the frequency of the oscillator changes, standing waves with different numbers of?minima?(nodes) and?maxima?(antinodes) form
Microwaves
- A microwave source is placed in line with a?reflecting plate?and a small?detector?between the two
- The reflector can be moved to and from the source to vary the stationary wave pattern formed
- By moving the?detector, it can pick up the minima (nodes) and maxima (antinodes) of the stationary wave pattern
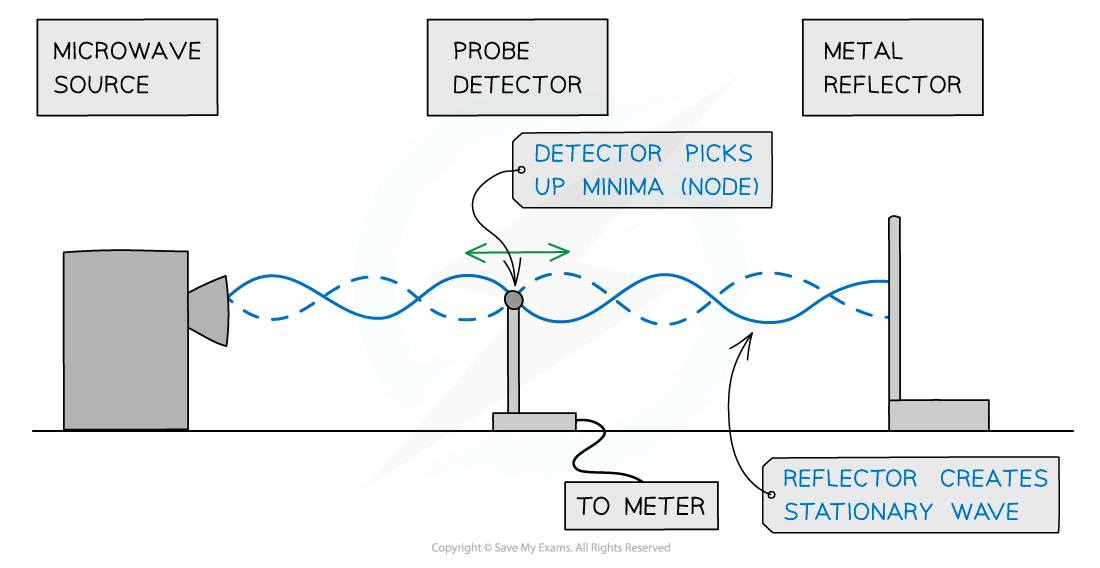
Using microwaves to demonstrate stationary waves
Air Columns
- The formation of stationary waves inside an air column can be produced by sound waves
- This is how musical instruments, such as clarinets and organs, work
- This can be demonstrated by placing a fine powder inside the air column and a loudspeaker at the open end
- At certain frequencies, the powder forms evenly spaced heaps along the tube, showing where there is?zero disturbance?as a result of the nodes of the stationary wave
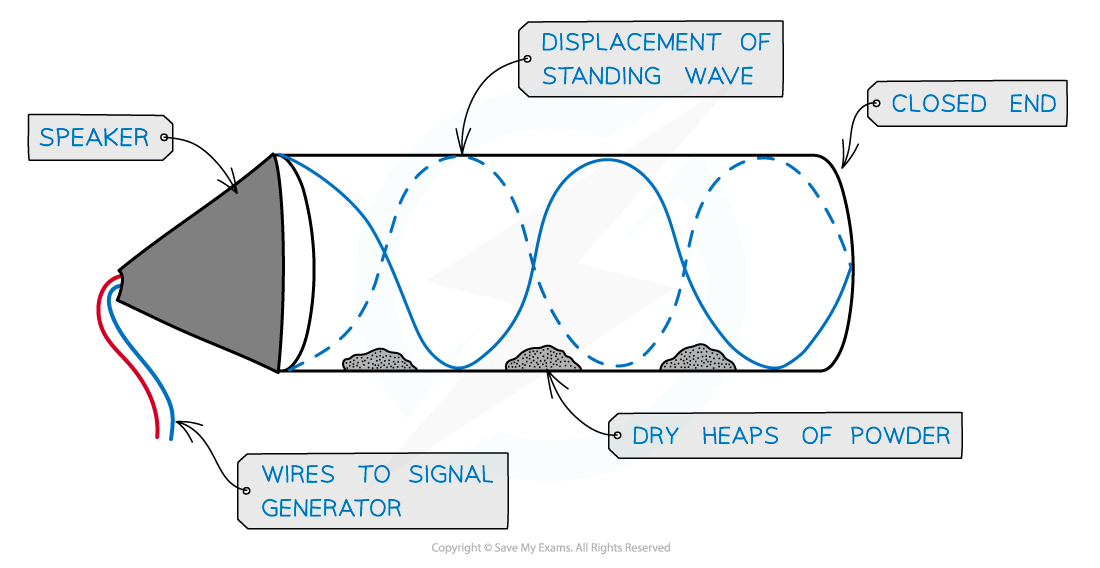
Stationary wave in an air column
- In order to produce a stationary wave, there must be a minima (node) at one end and a maxima (antinode) at the end with the loudspeaker
Nodes and Antinodes
- A stationary wave is made up?nodes?and?antinodes
- Nodes?are where there is no vibration
- Antinodes?are where the vibrations are at their maximum amplitude
- The nodes and antinodes?do not?move along the string. Nodes are fixed and antinodes only move in the vertical direction
- Between nodes, all points along the stationary wave are in phase
- The image below shows the nodes and antinodes on a snapshot of a stationary wave at a point in time
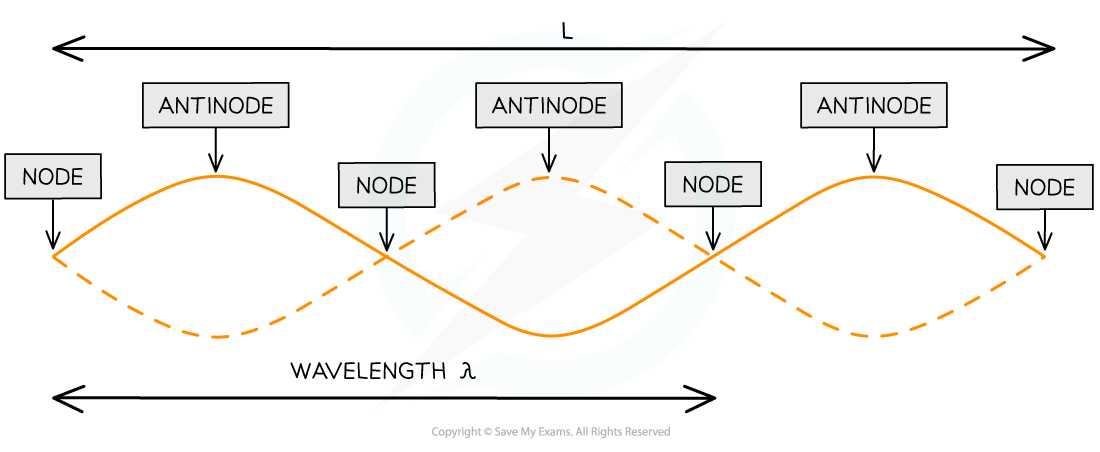
- L?is the length of the string
- 1 wavelength?λ?is only a portion of the length of the string
Worked Example
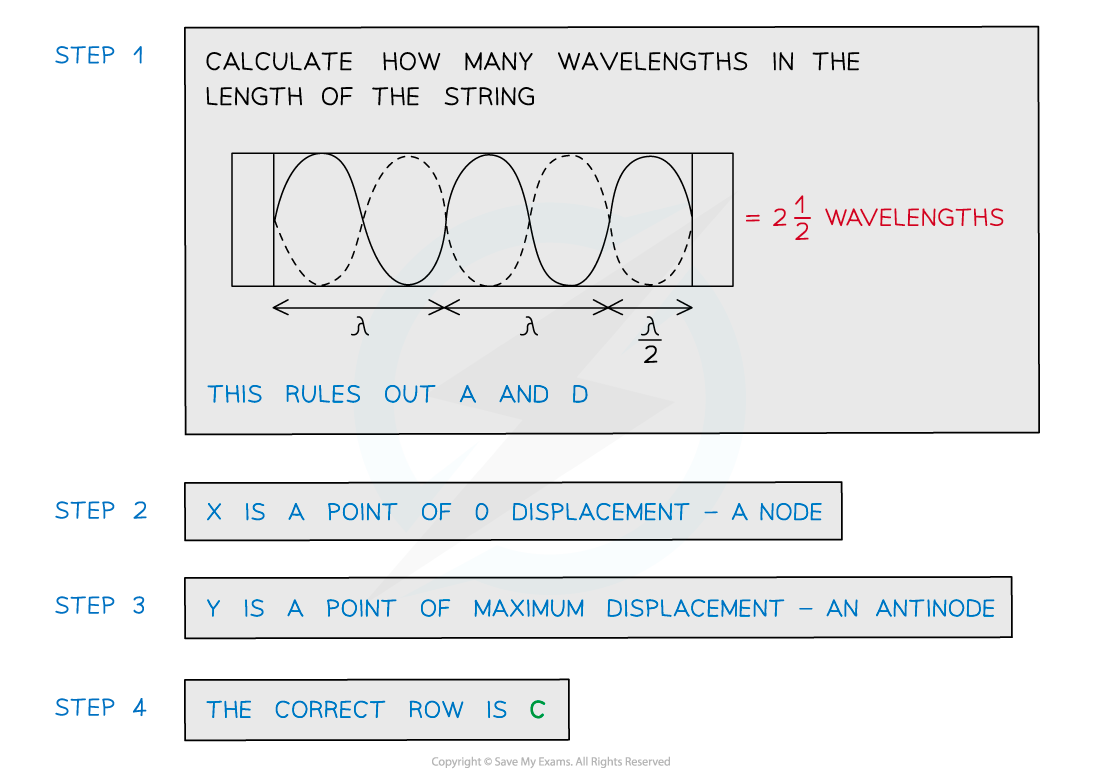
A stretched string is used to demonstrate a stationary wave, as shown in the diagram.

Which row in the table correctly describes the length of L and the name of?X?and?Y?
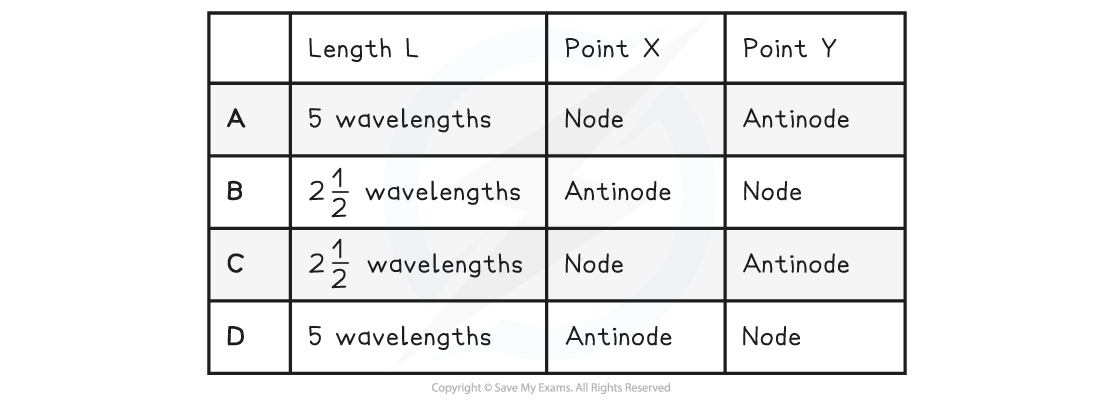
ANSWER:?C
Exam Tip
Always refer back to the experiment or scenario in an exam question e.g. the wave produced by a?loudspeaker?reflects at the end of a?tube. This reflected wave, with the same frequency, overlaps the initial wave to create a stationary wave.
Can't remember which is the node and which is the anti-node??Nodes occur at areas of?NO Disturbance!
轉載自savemyexams

最新發布
? 2025. All Rights Reserved. 滬ICP備2023009024號-1









