CIE A Level Physics復習筆記3.1.2 Force & Acceleration
Force & Acceleration
- As stated on the previous page, Newton's Second Law of Motion tells us that objects will accelerate if there is a resultant force acting upon them
- This acceleration will be in the same direction as this resultant force
Newton’s Second law equation
Resultant Force
- Since force is a vector, every force on a body has a magnitude and direction
- The resultant force is therefore the vector sum of all the forces acting on the body. The direction is given by either the positive or negative direction as shown in the examples below
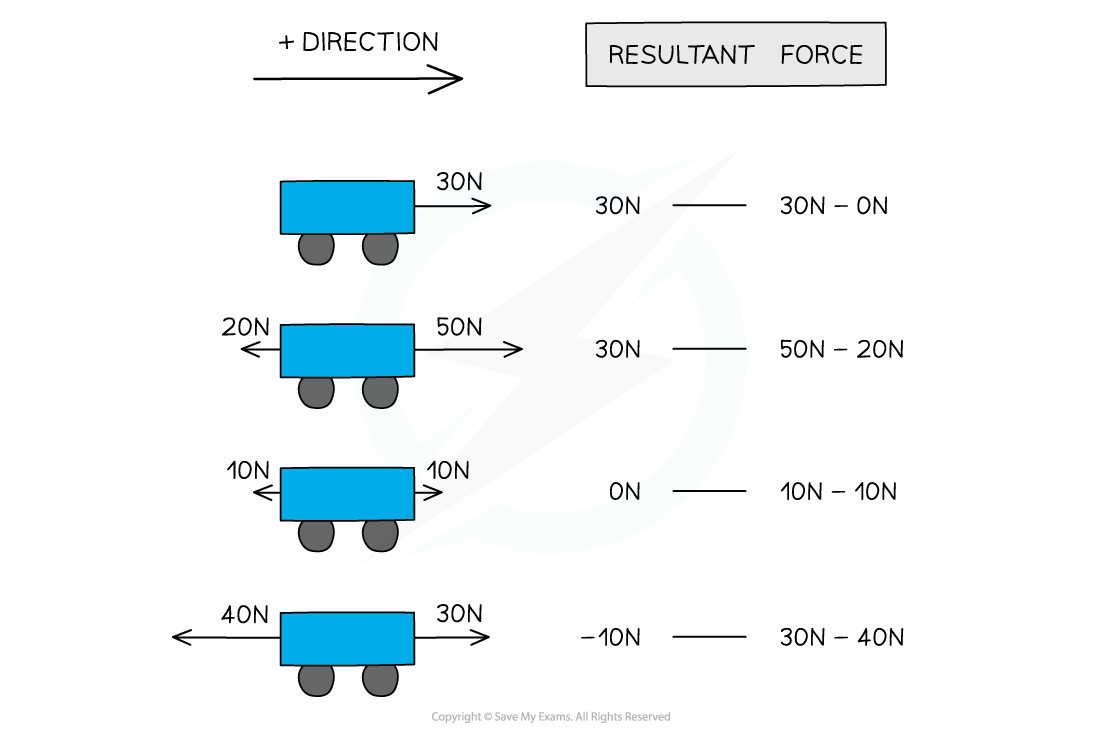
Resultant forces on a body
- The resultant force could also be at an angle, in which case addition of vectors is used to find the magnitude and direction of the resultant force.
- For more details on this, have a look at the page on “Scalars & Vectors”
Acceleration
- Given the mass, Newton’s Second Law means you can find the acceleration of an object
- Since acceleration is also a vector, it can be either positive or negative depending on the direction of the resultant force
- Negative acceleration is deceleration
- An object may continue in the same direction however with a resultant force in the opposite direction to its motion, it will slow down and eventually come to a stop
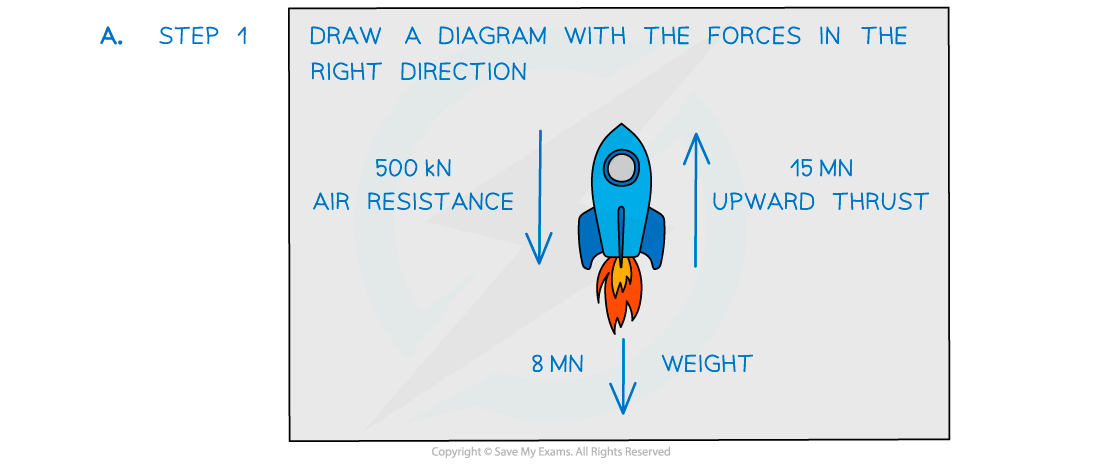
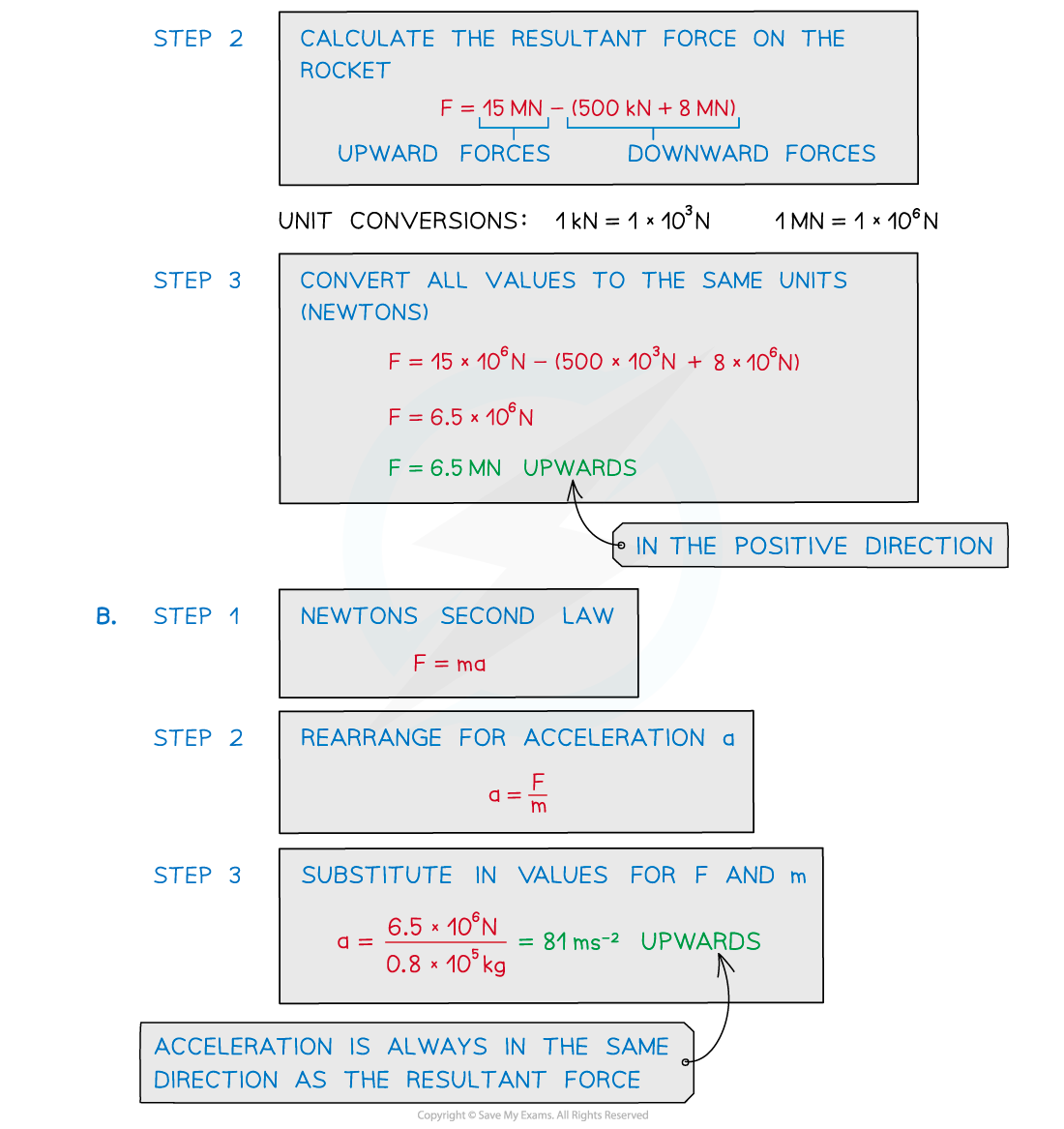
Worked Example
A rocket produces an upward thrust of 15 MN and has a weight of 8 MN.
A.??? When in flight, the force due to air resistance is 500 kN.
What is the resultant force on the rocket?
B.??? ?The mass of the rocket is 0.8 × 105?kg.
Calculate the acceleration of the rocket and the direction its going in.
Exam Tip
The direction you consider positive is your choice, as long the signs of the numbers (positive or negative) are consistent with this throughout the questionIt is a general rule to consider the direction of motion the object is travelling in as positive. Therefore all vectors in the direction of motion will be positive and opposing vectors such as drag forces, are negative.
轉載自savemyexams
國際競賽真題資源免費領取
美高學分項目重磅來襲！立即了解
