- 翰林提供學(xué)術(shù)活動、國際課程、科研項(xiàng)目一站式留學(xué)背景提升服務(wù)!
- 400 888 0080
IB DP Physics: HL復(fù)習(xí)筆記7.2.4 Binding Energy per Nucleon Curve
Binding Energy per Nucleon Curve
- In order to compare nuclear stability, it is more useful to look at the?binding energy per nucleon
- The binding energy per nucleon is defined as:
The binding energy of a nucleus divided by the number of nucleons in the nucleus
- A higher binding energy per nucleon indicates a higher stability
- In other words, it requires more energy to pull the nucleus apart
- Iron (A = 56) has the highest binding energy per nucleon, which makes it the?most stable of all the elements
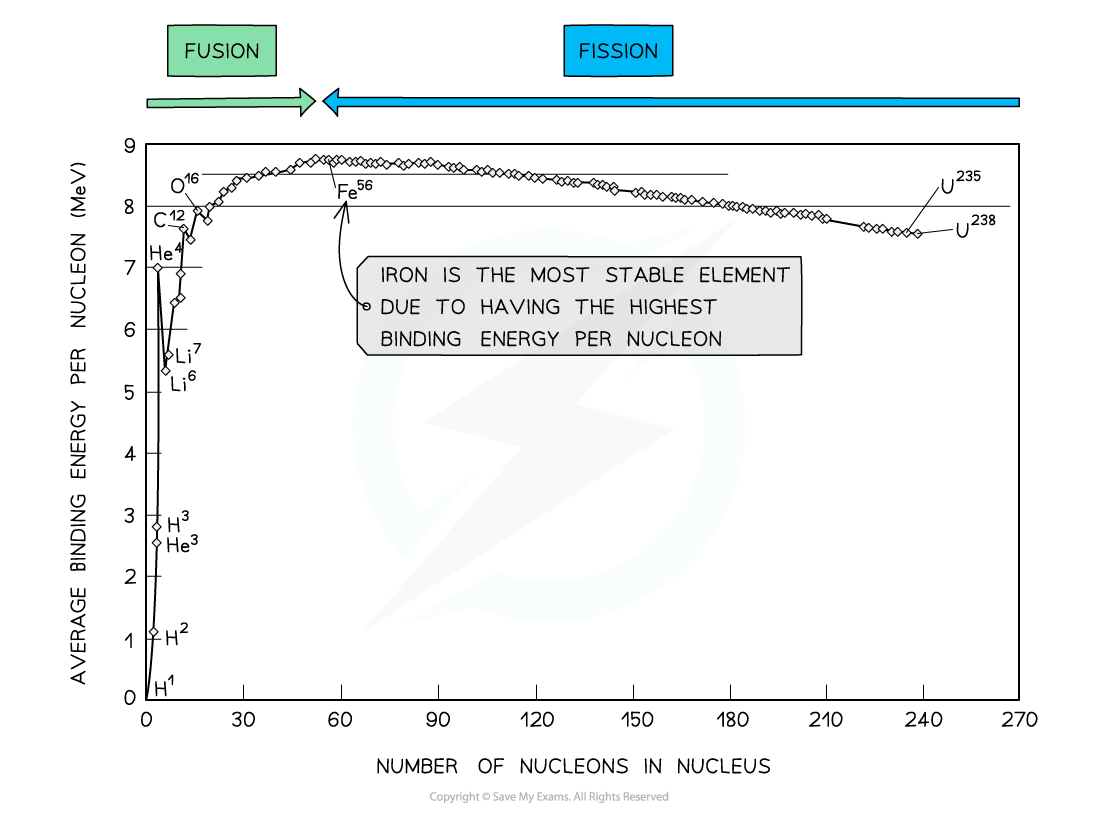
By plotting a graph of binding energy per nucleon against nucleon number, the stability of elements can be inferred
Key Features of the Graph
- At low values of A:
- Nuclei tend to have a lower binding energy per nucleon, hence, they are generally less stable
- This means the lightest elements have weaker electrostatic forces and are the most likely to undergo?fusion
- Helium (4He), carbon (12C) and oxygen (16O) do not fit the trend
- Helium-4 is a particularly stable nucleus hence it has a?high?binding energy per nucleon
- Carbon-12 and oxygen-16 can be considered to be three and four helium nuclei, respectively, bound together
- At high values of A:
- The general binding energy per nucleon is high and gradually decreases with A
- This means the heaviest elements are the most unstable and likely to undergo?fission
Comparing Fusion & Fission
- Fusion occurs at low values of A because:
- Attractive nuclear forces between nucleons dominate over repulsive electrostatic forces between protons
- In fusion, the mass of the nucleus that is created is slightly?less?than the total mass of the original nuclei
- The mass defect is equal to the binding energy that is released since the nucleus that is formed is more stable
- Fission occurs at high values of A because:
- Repulsive electrostatic forces between protons begin to dominate, and these forces tend to break apart the nucleus rather than hold it together
- In fission, an unstable nucleus is converted into more stable nuclei with a smaller total mass
- This difference in mass, the mass defect, is equal to the binding energy that is released
- Fusion releases much more energy per kg than fission
- The energy released is the difference in binding energy caused by the difference in mass between the reactant and products
- Hence, the greater the increase in binding energy, the greater the energy released
- At small values of A (fusion region), the gradient is?much steeper?compared to the gradient at large values of A (fission region)
- This corresponds to a larger binding energy per nucleon being released
Worked Example

Step 1: Calculate the mass defect Δm
Number of protons, Z = 26
Number of neutrons, A – Z = 56 – 26 = 30
Mass defect, Δm = Zmp?+ (A – Z)mn?– mtotal
Δm?= (26 × 1.673 × 10–27) + (30 × 1.675 × 10–27) – (9.288 × 10–26)
Δm?= 8.680 × 10–28?kg
Step 2: Calculate the binding energy?E?of the nucleus
Binding energy,?E?= Δmc2
E?= (8.680 × 10–28) × (3.00 × 108)2?= 7.812 × 10–11?J
Step 3: Calculate the binding energy per nucleon
 Worked Example
Worked Example
The equation below represents one possible decay of the induced fission of a nucleus of uranium-235.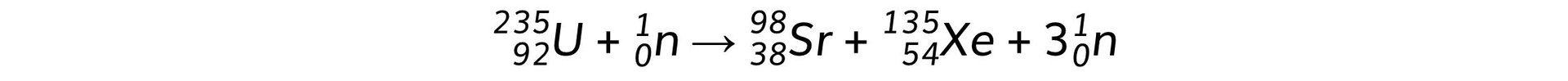 The graph shows the binding energy per nucleon plotted against nucleon number A.
The graph shows the binding energy per nucleon plotted against nucleon number A. Calculate the energy released:
Calculate the energy released:
a) By the fission process represented by the equation
b) When 1.0 kg of uranium, containing 3% by mass of U-235, undergoes fission
Part (a)
Step 1: Use the graph to identify each isotope’s binding energy per nucleon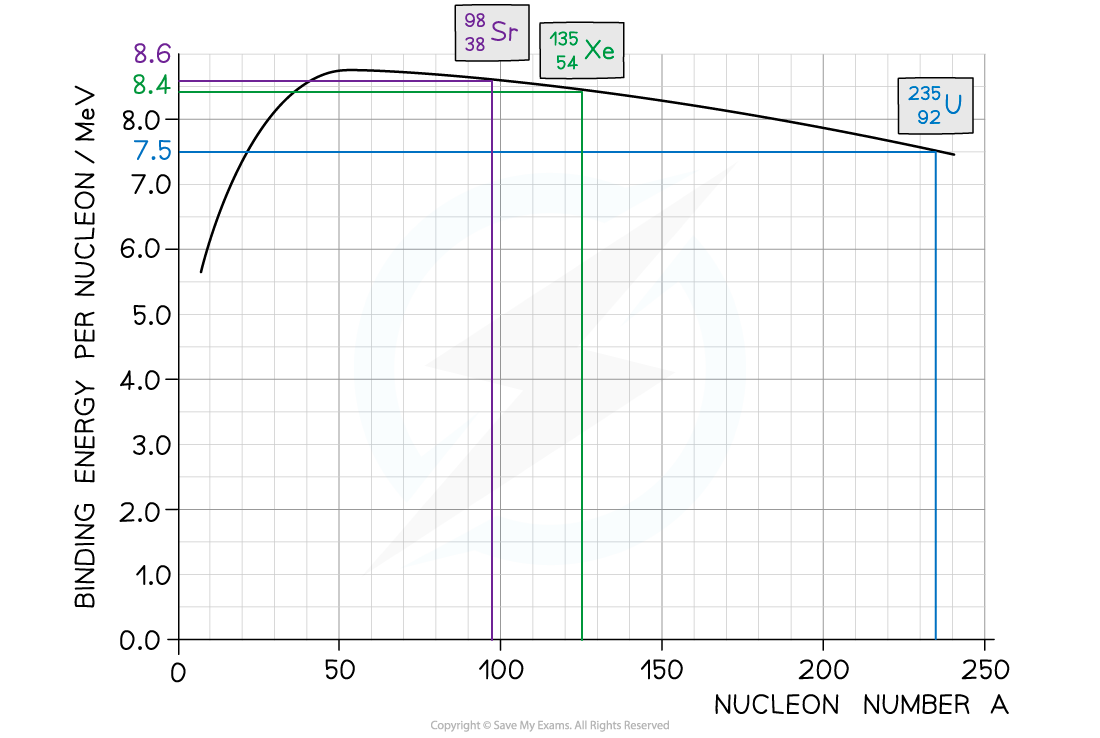
-
- Binding energy per nucleon (U-235) = 7.5 MeV
- Binding energy per nucleon (Sr-88) = 8.6 MeV
- Binding energy per nucleon (Xe-136) =?8.2 MeV
Step 2: Determine the binding energy of each isotope
Binding energy = Binding Energy per Nucleon × Mass Number
-
- Binding energy of U-235 nucleus = (235 × 7.5) = 1763 MeV
- Binding energy of Sr-88 = (88 × 8.6) = 757 MeV
- Binding energy of Xe-135 = (136 × 8.2) = 1115 MeV
Step 3: Calculate the energy released
Energy released = Binding energy after (Sr + Xe) – Binding energy before (U)
Energy released = (1115 + 757) – 1763 = 109 MeV
Part (b)
Step 1: Calculate the energy released by 1 mol of uranium-235
-
- There are?NA?(Avogadro’s number) atoms in 1 mol of U-235, which is equal to a mass of 235 g
- Energy released by 235 g of U-235 = (6 × 1023) × 214 MeV
Step 2: Convert the energy released from MeV to J
-
- 1 MeV = 1.6 × 10–13?J
- Energy released = (6 × 1023) × 214 × (1.6 × 10–13) = 2.05 × 1013?J
Step 3: Work out the proportion of uranium-235 in the sample
-
- 1 kg of uranium which is 3% U-235 contains 0.03 kg or 30 g of U-235
Step 4: Calculate the energy released by the sample
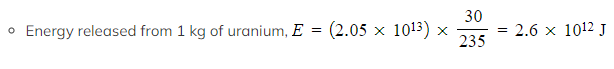 Exam Tip
Exam Tip
Checklist on what to include (and what not to include) in an exam question asking you to draw a graph of binding energy per nucleon against nucleon number:
- Do not begin your curve at A = 0, this is not a nucleus!
- Make sure to correctly label both axes AND units for binding energy per nucleon
- You will be expected to include numbers on the axes, mainly at the peak to show the position of iron (56Fe)
轉(zhuǎn)載自savemyexams

最新發(fā)布
? 2025. All Rights Reserved. 滬ICP備2023009024號-1









