- 翰林提供學(xué)術(shù)活動(dòng)、國(guó)際課程、科研項(xiàng)目一站式留學(xué)背景提升服務(wù)!
- 400 888 0080
IB DP Maths: AI HL復(fù)習(xí)筆記4.6.2 Unbiased Estimates
Unbiased Estimates
What is an unbiased estimator of a population parameter?
- An?estimator?is a?random variable?that is used to?estimate a population parameter
- An?estimate?is the value produced by the estimator when a sample is used
- An estimator is called unbiased if its expected value is equal to the population parameter
- An estimate from an unbiased estimator is called an?unbiased estimate
- This means that the?mean?of the?unbiased estimates?will get?closer?to the?population parameter?as?more samples?are taken
- The?sample mean?is an?unbiased estimate?for the?population mean
- The?sample variance?is?not an unbiased estimate?for the?population variance
- On average the sample variance will?underestimate?the population variance
- As the?sample size increases?the sample variance gets?closer to the unbiased?estimate
What are the formulae for unbiased estimates of the mean and variance of a population?
- A sample of?n?data values (x1, x2, ...?etc) can be used to find unbiased estimates for the mean and variance of the population
 Is?sn-1?an unbiased estimate for the standard deviation?
Is?sn-1?an unbiased estimate for the standard deviation?
- Unfortunately?sn-1?is not an unbiased estimate for the standard deviation of the population
- It is better to work with the unbiased variance rather than standard deviation
- There is not a formula for an unbiased estimate for the standard deviation that works for all populations
- Therefore you will not be asked to find one in your exam
How do I show the sample mean is an unbiased estimate for the population mean?
- You?do not need to learn this proof
- It is simply here to help with your understanding
- Suppose the population of X has mean?μ?and variance?σ2
- Take a sample of?n?observations
- X1,?X2,?..., Xn
- E(Xi) = μ
- Using the formula for a linear combination of?n?independent variables:
 Why is there a divisor of?n-1 in the unbiased estimate for the variance?
Why is there a divisor of?n-1 in the unbiased estimate for the variance?
- You?do not need to learn this proof
- It is simply here to help with your understanding
- Suppose the population of X has mean?μ?and variance?σ2
- Take a sample of?n?observations
- X1,?X2,?..., Xn
- E(Xi) = μ
- Var(Xi) = σ2
- Using the formula for a linear combination of?n?independent variables:

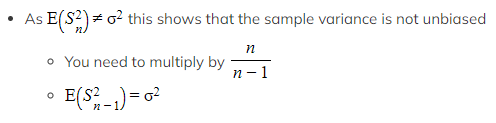
Exam Tip
Worked Example

轉(zhuǎn)載自savemyexams

最新發(fā)布
? 2025. All Rights Reserved. 滬ICP備2023009024號(hào)-1









