- 翰林提供學術活動、國際課程、科研項目一站式留學背景提升服務!
- 400 888 0080
AQA A Level Physics復習筆記6.5.2 Gas Laws
Ideal Gas Laws
- The ideal gas laws are the experimental relationships between?pressure?(P), volume (V) and temperature (T) of an ideal gas
- The mass and the number of molecules of the gas is assumed to be constant for all of these
Boyle’s Law
- If the temperature?T?of an ideal gas is constant, then?Boyle’s Law?is given by:
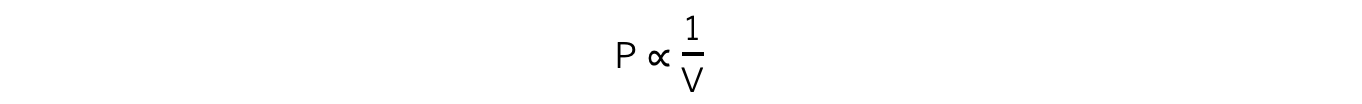
- This means the pressure is?inversely proportional?to the volume of a gas
- The relationship between the pressure and volume for a fixed mass of gas at constant temperature can also be written as:
P1V1?= P2V2
- Where:
- P1?= initial pressure (Pa)
- P2?= final pressure (Pa)
- V1?= initial volume (m3)
- V2?= final volume (m3)
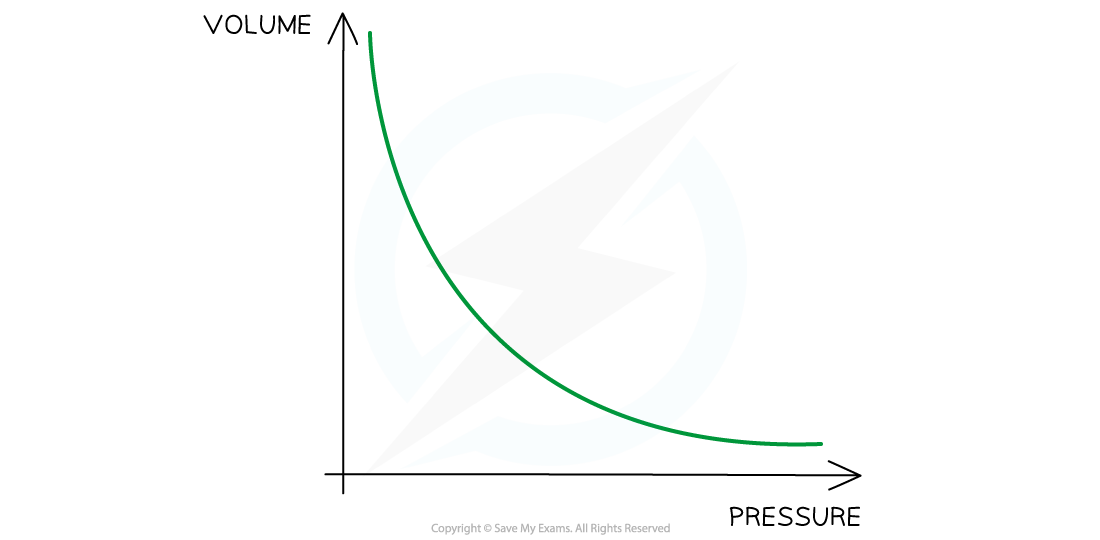
Boyle's Law graph representing pressure inversely proportional to volume
- If the temperature increases, the graph is further from the origin and vice versa
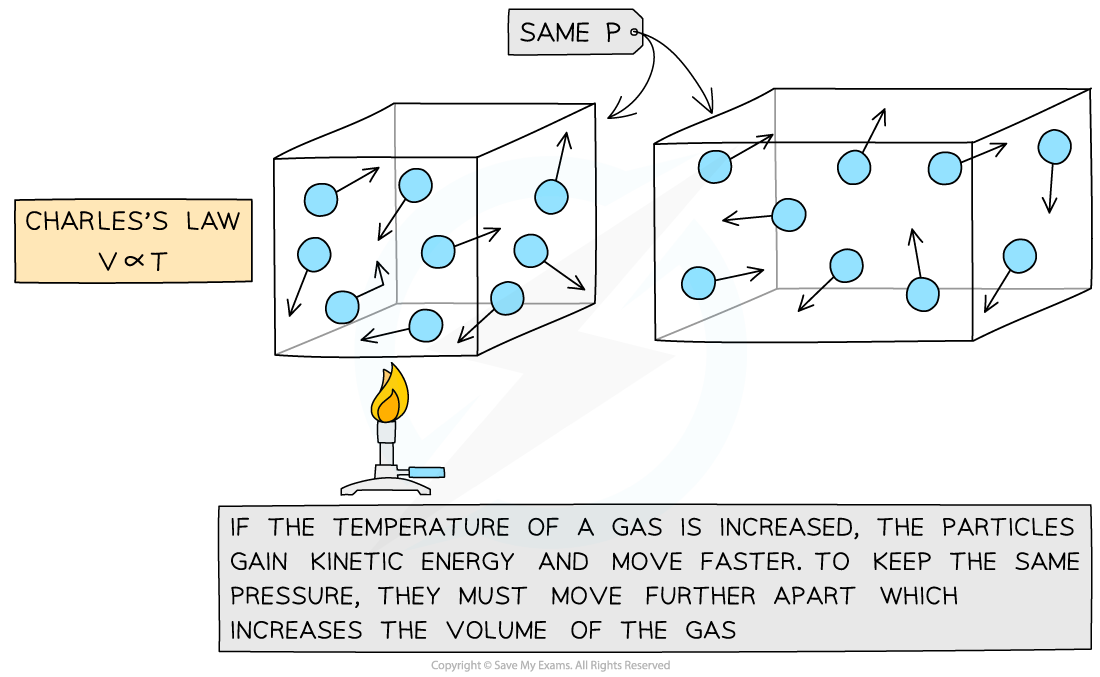
Charles's Law
- If the pressure?P?of an ideal gas is constant, then?Charles’s law?is given by:
V ∝ T
- This means the volume is?proportional?to the temperature of a gas
- The relationship between the volume and thermodynamic temperature for a fixed mass of gas at constant pressure can also be written as:
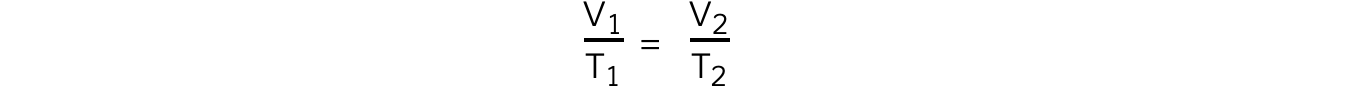
- Where:
- V1?= initial volume (m3)
- V2?= final volume (m3)
- T1?= initial temperature (K)
- T2?= final temperature (K)
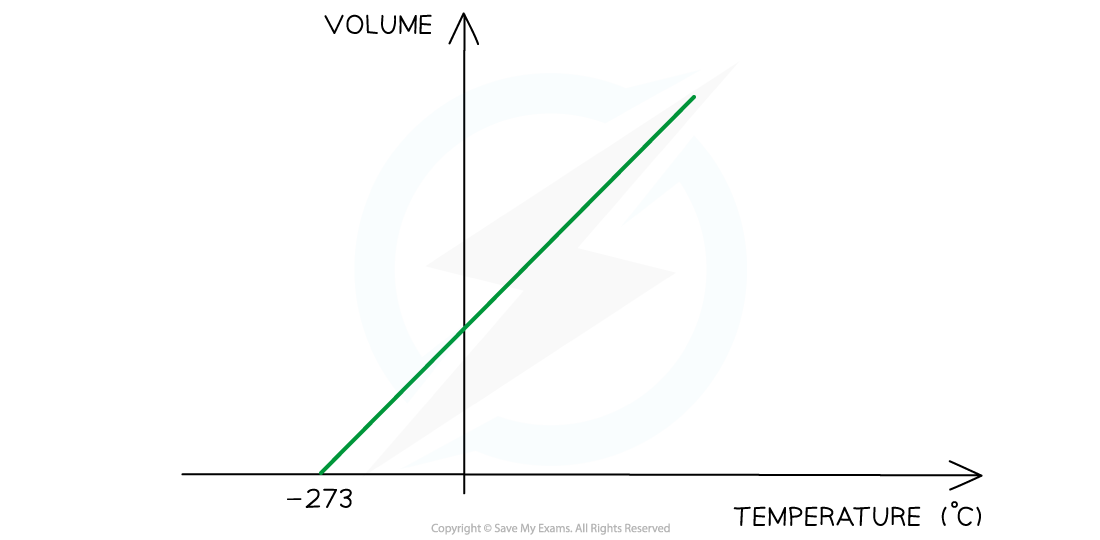
Charles's Law graph representing temperature (in °C) directly proportional to the volume
- The Charles's Law graph for temperature in?kelvin?against volume is identical except that is a straight line through the?origin
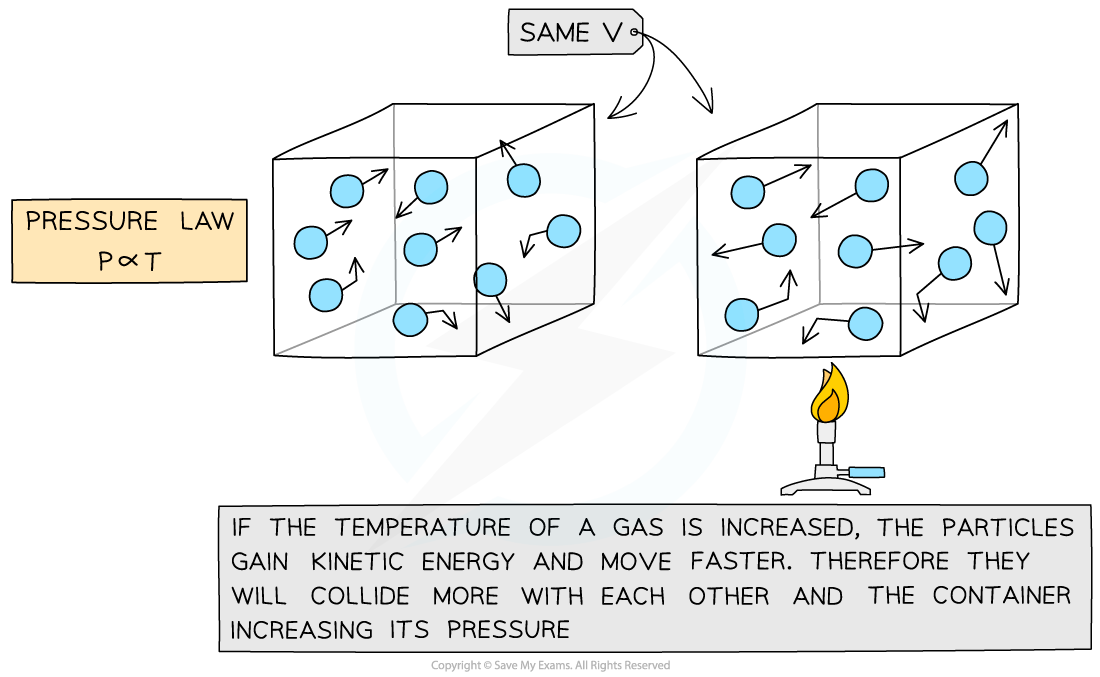
Pressure Law
- If the volume?V?of an ideal gas is constant, the?Pressure law?is given by:
P?∝?T
- This means the pressure is?proportional?to the temperature
- The relationship between the pressure and thermodynamic temperature for a fixed mass of gas at constant volume can also be written as:
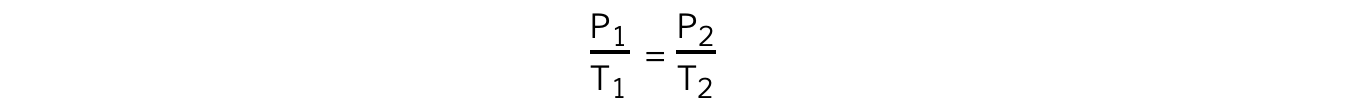
- Where:
- P1?= initial pressure (Pa)
- P2?= final pressure (Pa)
- T1?= initial temperature (K)
- T2?= final temperature (K)
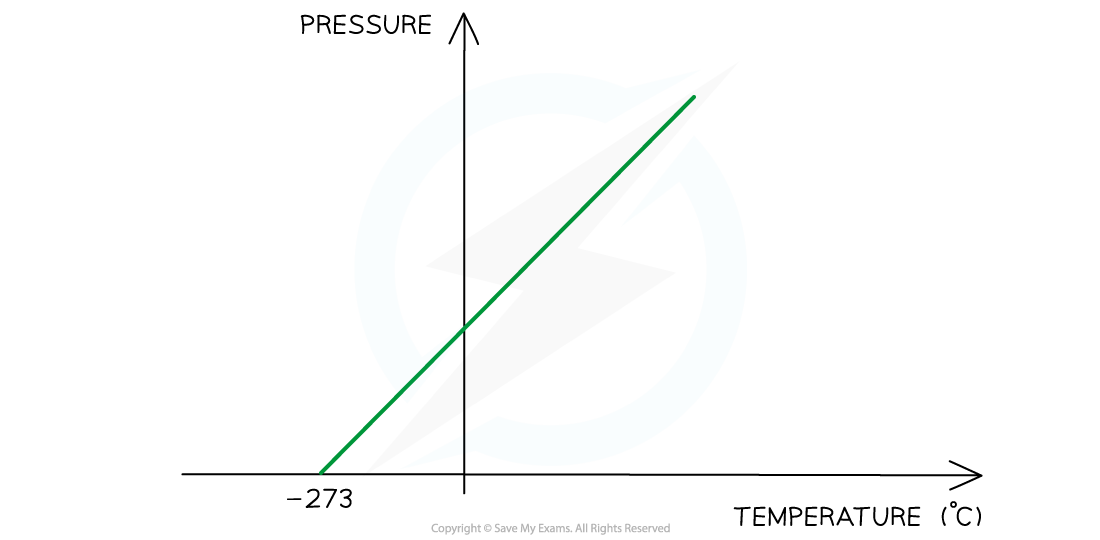
Pressure Law graph representing temperature (in °C) directly proportional to the volume
Worked Example
The pressure inside a bicycle tyre is 5.10 × 105?Pa when the temperature is 279 K.After the bicycle has been ridden, the temperature of the air in the tyre is 299 K. Calculate the new pressure in the tyre, assuming the volume is unchanged.

Exam Tip
Remember when using any ideal gas law, including the ideal gas equation, the temperature?T?must always be in?kelvin?(K)
Relationships Between Pressure, Volume & Temperature
- An?ideal gas?is one that obeys the relation:
pV?∝?T
- Where:
- p?=?pressure?of the gas (Pa)
- V?= volume of the gas (m3)
- T?=?thermodynamic temperature?(K)
- The molecules in a gas move around randomly at high speeds, colliding with surfaces and exerting pressure upon them
Gas molecules move about randomly at high speeds
- Imagine molecules of gas free to move around in a box
- The temperature of a gas is related to the average speed of the molecules:
- The hotter the gas, the faster the molecules move
- Hence the molecules collide with the surface of the walls more frequently
- Since force is the rate of change of?momentum:
- Each collision applies a?force?across the surface area of the walls
- The faster the molecules hit the walls, the greater the force on them
- Since pressure is the?force per unit area
- Higher temperature leads to higher pressure
- If the volume?V?of the box decreases, and the temperature?T?stays constant:
- There will be a smaller surface area of the walls and hence more collisions
- This also creates more pressure
- Since this equates to a greater force per unit area,?pressure?in an ideal gas is therefore defined by:
The frequency of collisions of the gas molecules per unit area of a container
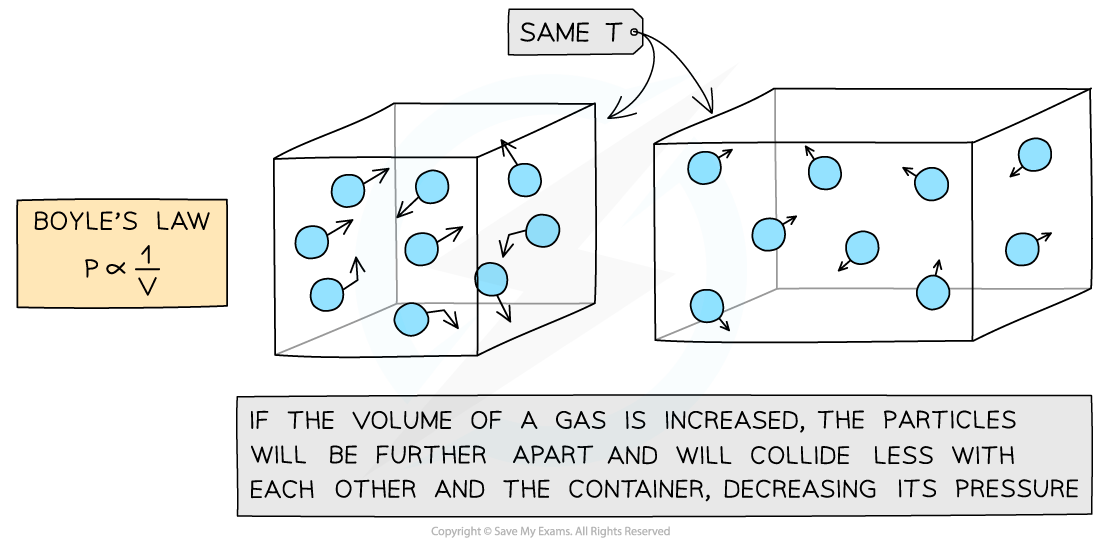
Molecular model of the three ideal gas laws
Worked Example
An ideal gas is in a container of volume 4.5 × 10-3?m3.The gas is at a temperature of 30 °C and a pressure of 6.2 × 105 Pa.Calculate the pressure of the ideal gas in the same container when it is heated to 40 °C.
Step 1: Ideal gas relation between pressure, volume and temperature
pV?∝?T
Step 2: Write the equation in full
pV?=?kT
-
- Where?k = the constant of proportionality
Step 3:?Rearrange for the constant of proportionality
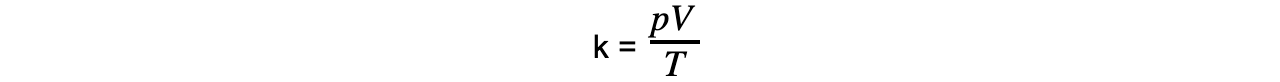
Step 4: Convert temperature T into Kelvin
θ °C + 273.15 = T K
30 °C + 273.15 = 303.15 K
Step 5:?Substitute in known value into constant of proportionality equation
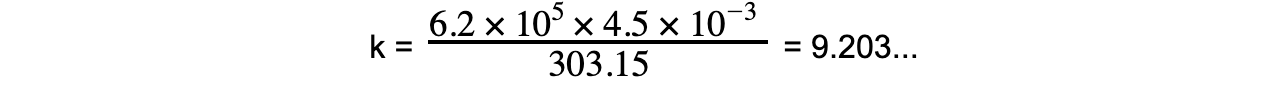
Step 6: Rearrange ideal gas relation equation for pressure
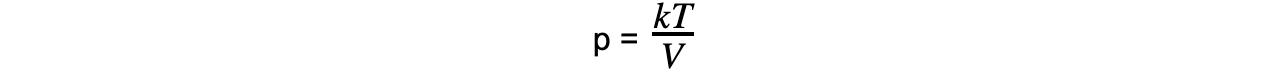
Step 7: Substitute in new values
k?= 9.203...
V?stays the same = 4.5 × 10-3?m3
T?= 40 °C?= 40 + 273.15 = 313.15 K
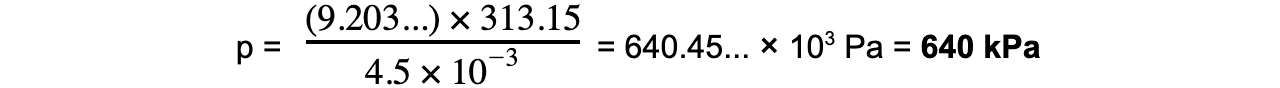
Exam Tip
Don’t round too early in your working out! In the worked example, the unrounded value of?k?is represented by “…” to show its full value is to be carried over to the next step of the calculation. On your calculator, this can be done by using the “ans” button instead of typing in the whole number.
轉載自savemyexams

最新發布
? 2025. All Rights Reserved. 滬ICP備2023009024號-1









