AQA A Level Chemistry復(fù)習(xí)筆記5.5.3 The Ionic Product of Water
The Ionic Product of Water
- In all aqueous solutions, an equilibrium exists in water where a few water molecules dissociate into protons and hydroxide ions
- We can derive an equilibrium constant for the reaction:
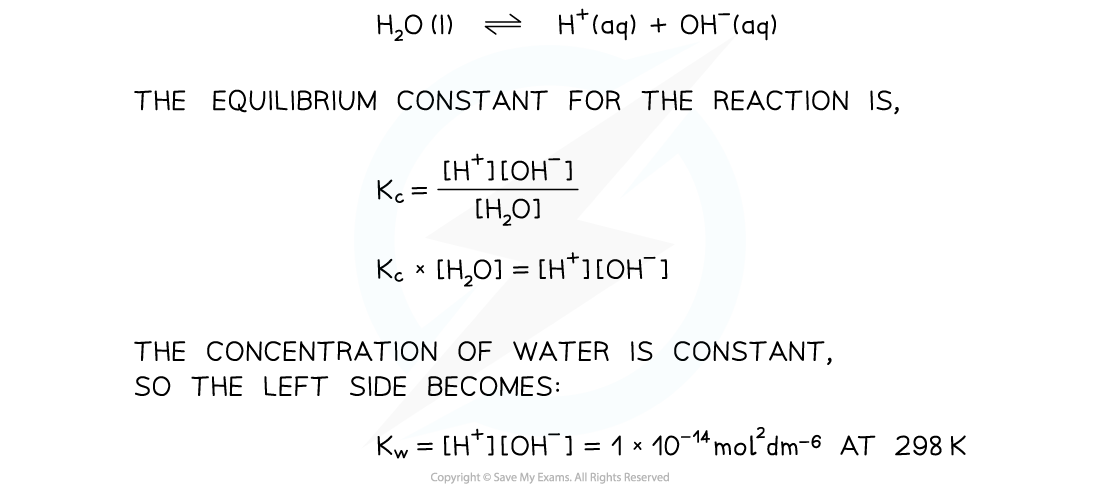
- This is a specific equilibrium constant called the?ionic product for water
- The product of the two ion concentrations is?always?1 x?10-14?mol2?dm-6
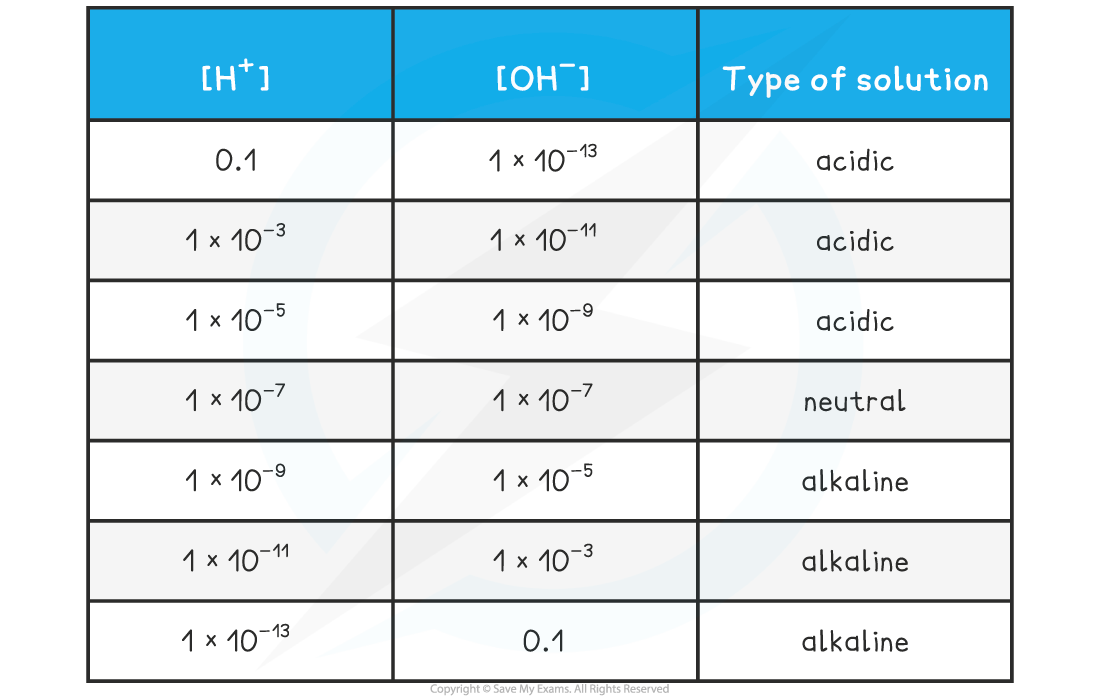
- This makes it straightforward to see the relationship between the two concentrations and the nature of the solution:
[H+] & [OH–] Table
pH of Strong Bases
Strong bases
- Strong bases?are completely?ionised?in solution
BOH (aq) → B+?(aq) + OH-?(aq)
- Therefore, the concentration of hydroxide ions [OH-] is?equal?to the concentration of base [BOH]
- Even strong alkalis have small amounts of H+?in solution which is due to the ionisation of water
- The concentration of OH-?in solution can be used to calculate the pH using the?ionic product of water
- Once the [H+] has been determined, the pH of the strong alkali can be founding using pH = -log[H+]
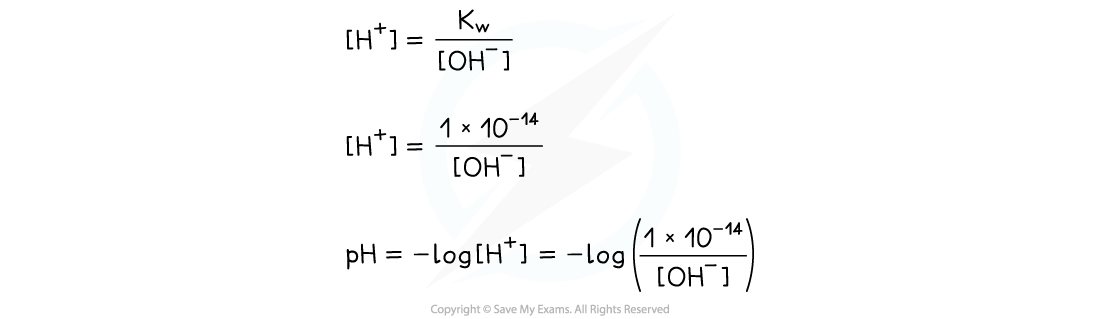
- Similarly, the ionic product of water can be used to find the concentration of OH-?ions in solution if [H+] is known, simply by dividing?Kw?by the?[H+
Worked Example
pH calculations of a strong alkaliQuestion 1:?Calculate the pH of 0.15?mol dm-3?sodium hydroxide, NaOHQuestion 2: Calculate the hydroxide concentration of a solution of sodium hydroxide when the pH is 10.50
Answer
Sodium hydroxide is a strong base which ionises as follows:
NaOH (aq) → Na+?(aq) + OH-?(aq)
Answer 1:
The pH of the solution is:
[H+] =?Kw??÷ [OH-]
[H+] = (1 x 10-14)?÷?0.15 = 6.66 x 10-14
pH = -log[H+]
= -log 6.66 x 10-14??= 13.17
Answer 2
Step 1:?Calculate hydrogen concentration by rearranging the equation for pH
pH = -log[H+]
[H+]= 10-pH
[H+]= 10-10.50
[H+]= 3.16 x 10-11?mol dm-3
Step 2:?Rearrange the?ionic product of water??to find the concentration of hydroxide ions
Kw?= [H+] [OH-]
[OH-]=?Kw??÷??[H+]
Step 3:?Substitute the values into the expression to find the concentration of hydroxide ions
Since?Kw?is 1 x 10-14?mol2?dm-6,
[OH-]= (1 x 10-14)÷? (3.16 x 10-11)
[OH-]=?3.16 x 10-4?mol dm-3
Worked Example
What is the pH of a solution of hydroxide ions of concentration 1.0 × 10?3?mol dm?3??Kw?= 1 × 10?14?mol2?dm-6
A. 3.00
B. 4.00
C. 10.00
D. 11.00
Answer
The correct option is?D.
-
- Since?Kw?= [H+] [OH–], rearranging gives [H+] ?=?Kw?÷ [OH–]
The concentration of ?[H+] is (1 × 10?14) ÷ (1.0 × 10?3) = 1.0 × 10?11?mol dm?3
[H+]= 10-pH
So the?pH = 11.00
Exam Tip
Always give the pH to two decimal places.
轉(zhuǎn)載自savemyexams
國(guó)際競(jìng)賽真題資源免費(fèi)領(lǐng)取
美高學(xué)分項(xiàng)目重磅來(lái)襲！立即了解
