2022AP物理C電磁學(xué)北美卷FRQ已放出，附考情分析

各位AP小伙伴們好呀~2022年5月10日進(jìn)行的AP物理C電磁學(xué)考試已經(jīng)結(jié)束，本場考試為線下紙筆考試，CB官網(wǎng)已更新了2022AP物理C電磁學(xué)北美FRQ真題。

2022年的AP物理C電磁考試已經(jīng)結(jié)束，今天官方放出了兩個Set的FRQ，我們趕緊一起來看看都考了哪些內(nèi)容吧！

試卷整體難度和知識點

兩個Set的相同題號考的知識點相近，第1題都是在考高斯定理和電場電勢的微積分關(guān)系，只不過Set 1是球?qū)ΨQ模型，Set 2是柱對稱模型；

第2題都是在考RC電路的實驗，都涉及了微分方程，且都是先充再放，只不過Set 1根據(jù)對數(shù)電壓-時間圖像求電容，Set 2是根據(jù)時間常數(shù)-電阻圖像求非理想電容的內(nèi)阻，但也都考了實驗誤差分析和圖像斜率變化；

第3題都是在考電流產(chǎn)生的磁場和電磁感應(yīng)，主要涉及磁場、磁通量計算、法拉第定律和楞次定律，只不過Set 1是長直導(dǎo)線周圍的不均磁場需要用積分計算磁通量，Set 2是螺線管里的勻強磁場，但都考了條件改變時感應(yīng)電流的變化分析。

整體難度中等，有的題非常簡單并且和往年題目極為相似，有個別問題較為新穎或有小坑。

與往年題目對比的點評

電場的題目應(yīng)該算簡單，2018年第1題也是絕緣球外面套一個導(dǎo)體球殼，用高斯定理算電場并畫圖，而柱對稱模型2013年也出過。

RC電路的先充后放問題去年剛剛考過，只不過去年更側(cè)重多個電阻電容串并聯(lián)的分析，而今年都是一個電阻一個電容，但在實驗設(shè)計和數(shù)據(jù)分析上做文章。

磁場的題也非常常規(guī)，Set 1非均勻磁場的磁通量去年MCQ考過，國際卷2017模擬題FRQ第3題也有，而Set 2螺線管電流變化在線圈中產(chǎn)生感應(yīng)在2019年Set 1的第3題也有考到，只不過2019年是線圈套在螺線管外，今年是線圈塞在螺線管里。這樣看來，如果同學(xué)們在考前刷過2018、2019、2021三年北美FRQ真題，對今年的考點應(yīng)該都有所應(yīng)對。

逐題點評

因為兩套題相同題號的考點類似，所以逐題點評按大題號順序進(jìn)行，每個序號內(nèi)分別講解Set 1和Set 2的兩版題目。

FRQ 1
Set 1: 一個均勻帶負(fù)電的絕緣球外面套了一個同心帶正電的導(dǎo)體球殼。
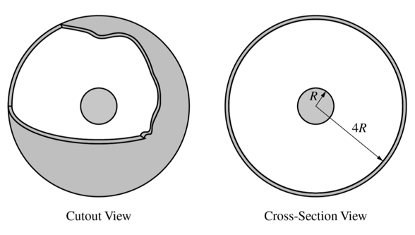(a) 求導(dǎo)體球外表面的電荷。
考點：導(dǎo)體靜電平衡，高斯定理，電荷守恒。
思路：根據(jù)靜電平衡的性質(zhì)，導(dǎo)體內(nèi)部沒有電場，根據(jù)高斯定理，球殼內(nèi)表面電荷與絕緣球加起來為0。再根據(jù)電荷守恒得到外表面電荷。

(b) 推導(dǎo)絕緣球內(nèi)部的電場表達(dá)式。
考點：高斯定理，電荷體積密度。
思路：在球內(nèi)做同心球型高斯面應(yīng)用高斯定理。電場在高斯面上處處相等且與面垂直，電通量為電場乘以球面積；內(nèi)部包圍的電荷量等于電荷體積密度乘以包圍的小球體積，其中體積密度可以用總電荷除以總體積得到。

(c) 已知絕緣球表面電場，求絕緣球和導(dǎo)體球殼中間某處的電場。
考點：高斯定理，平方反比規(guī)律。
思路：在絕緣球和導(dǎo)體球殼中間做高斯面應(yīng)用高斯定理可得電場遵循平方反比規(guī)律，距離變成兩倍則電場變成1/4。

(d) 求絕緣球表面和導(dǎo)體球殼內(nèi)表面的電勢差絕對值。
考點：電場電勢關(guān)系。
思路：對電場積分即得電勢差。

(e) 分別畫出電場和電勢與到球心距離的函數(shù)關(guān)系圖像。
考點：高斯定理，電場電勢關(guān)系。
思路：根據(jù)高斯定理可以先求得電場的變化規(guī)律（前幾問已求出一部分），再根據(jù)電場等于電勢的負(fù)導(dǎo)數(shù)，可以從電場確定電勢圖像的斜率如何變化，從而畫出電勢的變化趨勢。例如電場如果為負(fù)（指向球心）且線性增大，那電勢的斜率為正且增大，為上凹曲線。

掃碼添加翰林顧問老師，可一對一制定國際課程規(guī)劃
【免費領(lǐng)取】AP備考資料合集~

Set 2: 一個無限長均勻帶正電的絕緣圓柱外面套了一個同軸帶正電的導(dǎo)體圓柱殼。
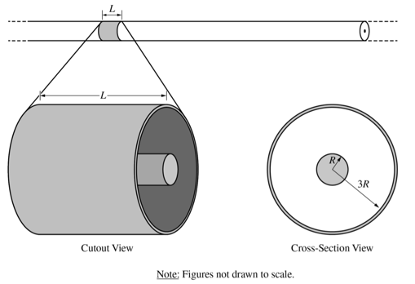(a) 求一段導(dǎo)體圓柱殼外表面的電荷。
考點：導(dǎo)體靜電平衡，高斯定理，電荷守恒。
思路：根據(jù)靜電平衡，導(dǎo)體內(nèi)部沒有電場。根據(jù)高斯定理，圓柱殼內(nèi)表面電荷與絕緣圓柱加起來為0。再根據(jù)電荷守恒，得到外表面電荷。

(b) 推導(dǎo)絕緣圓柱內(nèi)部的電場表達(dá)式。
考點：高斯定理，電荷體積密度。
思路：在圓柱內(nèi)做圓柱形高斯面應(yīng)用高斯定理，電場在側(cè)表面上處處相等且垂直于側(cè)表面，電通量為電場乘以圓柱的側(cè)面積；內(nèi)部包圍的電荷量為電荷體積密度乘以包圍的小圓柱體積，其中體積密度可以用總電荷除以總體積得到。

(c) 已知絕緣圓柱表面電場，求絕緣圓柱和導(dǎo)體圓柱殼中間某處的電場。
考點：高斯定理，反比規(guī)律。
思路：在絕緣圓柱和導(dǎo)體球圓柱殼中間做高斯面應(yīng)用高斯定理可得電場與到軸線距離成一次反比規(guī)律，距離變成兩倍則電場變成1/2。

(d) 求絕緣圓柱和導(dǎo)體圓柱殼內(nèi)表面的電勢差絕對值。
考點：電場電勢關(guān)系。
思路：對電場積分即得電勢差。

(e) 分別畫出電場和電勢與到軸線距離的函數(shù)關(guān)系圖像。
考點：高斯定理，電場電勢關(guān)系。
思路：根據(jù)高斯定理可以先求得電場的變化規(guī)律（前幾問已求出一部分），再根據(jù)電場等于電勢的負(fù)導(dǎo)數(shù)，可以從電場確定電勢圖像的斜率如何變化，從而畫出電勢的變化趨勢。例如電場如果為正（沿半徑向外）且線性增大，那電勢的斜率為負(fù)、電勢減小，且絕對值增大，為上凸曲線。

FRQ 2
Set 1:用一個可變電容研究放電時的電壓變化。給了一個理想電池，一個電壓表，一個電阻，第一個可變電容，和若干開關(guān)。

(a) 畫一個電路圖，既可以用來給電容充電，還可以用來研究放電電壓。
考點：RC充放電電路。
思路：電路中應(yīng)該至少包含兩個回路，一個包含電源用于充電，一個不含電源用于放電，兩者共用一個電阻-電容支路。需要至少兩個開關(guān)，一個控制充電，一個控制放電。另外電壓表應(yīng)該并聯(lián)接在電容器兩端。

(b) 證明放電時電容器電壓隨時間變化的函數(shù)表達(dá)式。
考點：基爾霍夫定律，RC電路的微分方程。
思路：對RC放電回路列基爾霍夫定律，把電流i寫成dq/dt得到微分方程，求解出q(t)進(jìn)而得到V(t)。需要注意兩點：(1)電流正方向規(guī)定為流向正極板才有i=dq/dt，實際放電電流為負(fù)；如果規(guī)定放電電流方向為正，則i=-dq/dt。(2)電容器放電的初始電壓等于充滿電的穩(wěn)態(tài)電壓，亦等于電源電壓。

(c) 根據(jù)實驗數(shù)據(jù)畫出了散點圖，縱軸為電容電壓與初始電壓之比的自然對數(shù)ln(V/V0)，橫軸是時間，讓我們畫出最佳擬合線，并用其求電容。
考點：指數(shù)函數(shù)線性化，最佳擬合線斜率的利用。
思路：將上一小問的表達(dá)式變形后可以得到直線的斜率所代表的物理量是-1/RC，畫出擬合線后，在線上取兩點求斜率，C=-1/(R*slope)。

(d) 調(diào)節(jié)可變電容器的平行板面積，重復(fù)實驗，問直線的斜率會更陡峭、更平緩、還是不變，并解釋原因。
考點：電容的決定式，改變條件下的斜率分析。
思路：根據(jù)電容決定式，面積增大，電容增大；再根據(jù)斜率=-1/RC，C增大斜率絕對值減小，所以是less steep。

(e) 將理想電池?fù)Q成一個有內(nèi)阻的電池，問斜率和截距是否變化，并解釋原因。
考點：非理想電源的內(nèi)阻，RC放電。
思路：電源的內(nèi)阻不會改變充電時的穩(wěn)態(tài)電壓，也不改變放電電路的時間常數(shù)，所以圖像的斜率和截距都不變。

Set 2: 做實驗確定一個非理想（含內(nèi)阻）電容器的內(nèi)阻。給了一個理想電池，一個電流表，一個可變電阻，第一個電容，和若干開關(guān)。

(a) 畫一個電路圖，既可以用來給電容充電，還可以用來研究放電電流。
考點：RC充放電電路。
思路：電路中應(yīng)該至少包含兩個回路，一個包含電源用于充電，一個不含電源用于放電，兩者共用一個電阻-電容支路。需要至少兩個開關(guān)，一個控制充電，一個控制放電。另外電流表應(yīng)該與電容器直接串聯(lián)。

(b) 證明放電時通過電容器的電流隨時間變化的函數(shù)表達(dá)式。
考點：基爾霍夫定律，RC電路的微分方程。
思路：對RC放電回路列基爾霍夫定律，把電流i寫成dq/dt得到微分方程，求解出q(t)進(jìn)而得到i(t)。需要注意兩點：(1)電流正方向規(guī)定為流向正極板才有i=dq/dt，實際放電電流為負(fù)；如果規(guī)定放電電流方向為正，則i=-dq/dt。(2)電容器放電的初始電壓等于充滿電的穩(wěn)態(tài)電壓，亦等于電源電壓。

(c) 根據(jù)實驗數(shù)據(jù)畫出了散點圖，縱軸為時間常數(shù)τ，橫軸為可變電阻的阻值R，讓我們畫出最佳擬合線，并用其求電容。
考點：時間常數(shù)，最佳擬合線斜率和截距的利用。
思路：在上一小問的表達(dá)式中可以看出時間常數(shù)τ=(R+r)C，變形后可以得到直線的斜率所代表的物理量是C、縱截距所代表的物理量是r*C，畫出擬合線后，在線上取兩點求斜率得到C，找縱軸交點求截距，則電容內(nèi)阻r=intercept/C。也可以反向延長找到直線與橫軸負(fù)半軸的交點直接得到內(nèi)阻，但因為給定的坐標(biāo)格不包含負(fù)半軸所以一般不這么做。

(d) 如果電流表也有內(nèi)阻，試分析電容器的真實內(nèi)阻與實驗值的差異。
考點：電流表內(nèi)阻，誤差分析。
思路：如果電流表有內(nèi)阻，實驗值應(yīng)為電流表內(nèi)阻和電容器內(nèi)阻之和，大于電容器內(nèi)阻。

(e) 改變可變電阻器的電阻范圍，問斜率如何變化。
考點：改變條件下的誤差分析。
思路：改變橫坐標(biāo)的取值范圍，斜率不變，仍是C。

FRQ 3
Set 1: 一個連有燈泡的矩形線框放在通電長直導(dǎo)線附近，導(dǎo)線中的電流先減小再反向增大。
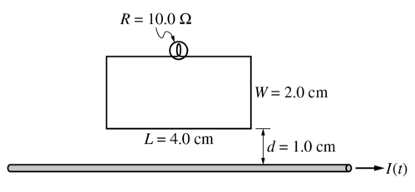(a) 問直導(dǎo)線電流反向時矩形線框中感應(yīng)電流的方向。
考點：電流產(chǎn)生的磁場，楞次定律。
思路：根據(jù)右手定則，直導(dǎo)線在上方線框中產(chǎn)生的磁場是先向外減小、再向里增大的。根據(jù)楞次定律，感應(yīng)磁場應(yīng)該一直向外，不要被“反向”這個瞬間迷惑。再根據(jù)右手定則判斷感應(yīng)電流方向為逆時針。

(b) 計算某時刻線框中的磁通量。
考點：不均勻磁場中磁通量的計算。
思路：直導(dǎo)線周圍的磁場和距離成反比，需要用微元法，將線框分成無數(shù)個細(xì)橫條，計算每個面積微元上的磁通量，再積分。

(c) 計算某時刻通過燈泡電流。
考點：法拉第定律。
思路：利用上一問的方法得到磁通量隨時間變化的關(guān)系，根據(jù)法拉第定律計算感應(yīng)電動勢，除以電阻即得到電流。

(d) 測量發(fā)現(xiàn)實際電流比上一問的計算值大，選擇一個可能的原因。
考點：法拉第定律。
思路：直導(dǎo)線中電流變化得比預(yù)期快會導(dǎo)致線框中磁通量變化率偏大，從而感應(yīng)電流偏大。

(e) 將矩形線框旋轉(zhuǎn)90度使短邊平行于長直導(dǎo)線，比較同一時刻的感應(yīng)電流和c問中的大小。
考點：電流產(chǎn)生的磁場，磁通量，法拉第定律。
思路：距離到導(dǎo)線越遠(yuǎn)磁場越小，旋轉(zhuǎn)后更多面積微元遠(yuǎn)離導(dǎo)線，總磁通量和電流的比例系數(shù)變小，感應(yīng)電動勢和感應(yīng)電流也相應(yīng)變小。

Set 2: 一個單匝線圈放在螺線管中，螺線管的電流在線性增大。
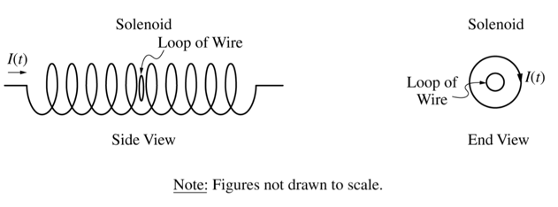(a) 問線圈中感應(yīng)電流的方向。
考點：電流產(chǎn)生的磁場，楞次定律。
思路：根據(jù)右手定則，在側(cè)視圖中螺線管在線圈中產(chǎn)生的磁場是向里增大的。根據(jù)楞次定律，感應(yīng)磁場應(yīng)該與之相反向外。再根據(jù)右手定則判斷感應(yīng)電流方向逆時針。

(b) 計算某時刻線圈中的感應(yīng)電流。
考點：磁通量計算，法拉第定律。
思路：根據(jù)螺線管磁場公式計算線圈中磁通量，再根據(jù)法拉第定律計算感應(yīng)電動勢，再用歐姆定律得到電流。

(c) 計算一段時間線圈消耗的能量。
考點：能量和功率。
思路：利用感應(yīng)電動勢或感應(yīng)電流得到功率，乘以時間得到消耗的能量。

(d) 測量發(fā)現(xiàn)實際電流比b問的計算值小，選擇一個可能的原因。
考點：法拉第定律。
思路：線圈平面與螺線管軸線不垂直會導(dǎo)致磁通量變化率偏小進(jìn)而感應(yīng)電流偏小。

(e) 將線圈半徑變成兩倍，問感應(yīng)電流和b中的比值。
考點：磁通量，法拉第定律，電阻的決定式
思路：線圈半徑變兩倍，面積變4倍，感應(yīng)電動勢變4倍。但是題目暗示了我們線圈周長變成了2倍，電阻也變成了2倍，所以感應(yīng)電流應(yīng)該只變成2倍。

寫在最后
以上就是北美考情的分析了，對于備考明年考試的同學(xué)來說，應(yīng)當(dāng)注意對基礎(chǔ)公式和模型的掌握，AP的出題風(fēng)格并不會有太激進(jìn)或太靈活的變化，和課內(nèi)的呼應(yīng)比較好。不過需要基本功扎實，尤其是公式推導(dǎo)和微積分的計算要足夠熟練。