Home » 國際競賽 » 數學國際競賽 » AMC美國數學競賽 » Details

2008AMC10A真題與答案解析

Category: AMC美國數學競賽, 國際競賽 Date: 2019年12月4日下午5:04

2008AMC10A真題

答案解析請參考文末

Problem 1

A bakery owner turns on his doughnut machine at? $text{8:30} {smalltext{AM}}$ . At? $text{11:10} {smalltext{AM}}$ ?the machine has completed one third of the day's job. At what time will the doughnut machine complete the job?

$mathrm{(A)} text{1:50} {smalltext{PM}}qquadmathrm{(B)} text{3:00} {smalltext{PM}}qquadmathrm{(C)} text{3:30} {smalltext{PM}}qquadmathrm{(D)} text{4:30} {smalltext{PM}}qquadmathrm{(E)} text{5:50} {smalltext{PM}}$

Problem 2

A square is drawn inside a rectangle. The ratio of the width of the rectangle to a side of the square is? $2:1$ . The ratio of the rectangle's length to its width is? $2:1$ . What percent of the rectangle's area is in the square?

$mathrm{(A)} 12.5qquadmathrm{(B)} 25qquadmathrm{(C)} 50qquadmathrm{(D)} 75qquadmathrm{(E)} 87.5$

Problem 3

For the positive integer? $n$ , let? $langle nrangle$ ?denote the sum of all the positive divisors of? $n$ ?with the exception of? $n$ ?itself. For example,? $langle 4rangle=1+2=3$ ?and? $langle 12 rangle =1+2+3+4+6=16$ . What is? $langlelanglelangle 6rangleranglerangle$ ?

$mathrm{(A)} 6qquadmathrm{(B)} 12qquadmathrm{(C)} 24qquadmathrm{(D)} 32qquadmathrm{(E)} 36$

Problem 4

Suppose that? $tfrac{2}{3}$ ?of? $10$ ?bananas are worth as much as? $8$ ?oranges. How many oranges are worth as much as? $tfrac{1}{2}$ ?of? $5$ ?bananas?

$mathrm{(A)} 2qquadmathrm{(B)} frac{5}{2}qquadmathrm{(C)} 3qquadmathrm{(D)} frac{7}{2}qquadmathrm{(E)} 4$

Problem 5

Which of the following is equal to the product $[frac{8}{4}cdotfrac{12}{8}cdotfrac{16}{12}cdotcdotscdotfrac{4n+4}{4n}cdotcdotscdotfrac{2008}{2004}?]$

$mathrm{(A)} 251qquadmathrm{(B)} 502qquadmathrm{(C)} 1004qquadmathrm{(D)} 2008qquadmathrm{(E)} 4016$

Problem 6

A triathlete competes in a triathlon in which the swimming, biking, and running segments are all of the same length. The triathlete swims at a rate of 3 kilometers per hour, bikes at a rate of 20 kilometers per hour, and runs at a rate of 10 kilometers per hour. Which of the following is closest to the triathlete's average speed, in kilometers per hour, for the entire race?

$mathrm{(A)} 3qquadmathrm{(B)} 4qquadmathrm{(C)} 5qquadmathrm{(D)} 6qquadmathrm{(E)} 7$

Problem 7

The fraction $[frac{left(3^{2008}right)^2-left(3^{2006}right)^2}{left(3^{2007}right)^2-left(3^{2005}right)^2}]$ simplifies to which of the following?

$mathrm{(A)} 1qquadmathrm{(B)} frac{9}{4}qquadmathrm{(C)} 3qquadmathrm{(D)} frac{9}{2}qquadmathrm{(E)} 9$

Problem 8

Heather compares the price of a new computer at two different stores. Store? $A$ ?offers? $15%$ ?off the sticker price followed by a? $textdollar90$ ?rebate, and store? $B$ ?offers? $25%$ ?off the same sticker price with no rebate. Heather saves? $textdollar15$ ?by buying the computer at store? $A$ ?instead of store? $B$ . What is the sticker price of the computer, in dollars?

$mathrm{(A)} 750qquadmathrm{(B)} 900qquadmathrm{(C)} 1000qquadmathrm{(D)} 1050qquadmathrm{(E)} 1500$

Problem 9

Suppose that $[frac{2x}{3}-frac{x}{6}]$ is an integer. Which of the following statements must be true about? $x$ ?

$mathrm{(A)} text{It is negative.}qquadmathrm{(B)} text{It is even, but not necessarily a multiple of 3.}\qquadmathrm{(C)} text{It is a multiple of 3, but not necessarily even.}\qquadmathrm{(D)} text{It is a multiple of 6, but not necessarily a multiple of 12.}\qquadmathrm{(E)} text{It is a multiple of 12.}$

Problem 10

Each of the sides of a square? $S_1$ ?with area? $16$ ?is bisected, and a smaller square? $S_2$ ?is constructed using the bisection points as vertices. The same process is carried out on? $S_2$ ?to construct an even smaller square? $S_3$ . What is the area of? $S_3$ ?

$mathrm{(A)} frac{1}{2}qquadmathrm{(B)} 1qquadmathrm{(C)} 2qquadmathrm{(D)} 3qquadmathrm{(E)} 4$

Problem 11

While Steve and LeRoy are fishing 1 mile from shore, their boat springs a leak, and water comes in at a constant rate of 10 gallons per minute. The boat will sink if it takes in more than 30 gallons of water. Steve starts rowing toward the shore at a constant rate of 4 miles per hour while LeRoy bails water out of the boat. What is the slowest rate, in gallons per minute, at which LeRoy can bail if they are to reach the shore without sinking?

$mathrm{(A)} 2qquadmathrm{(B)} 4qquadmathrm{(C)} 6qquadmathrm{(D)} 8qquadmathrm{(E)} 10$

Problem 12

In a collection of red, blue, and green marbles, there are? $25%$ ?more red marbles than blue marbles, and there are? $60%$ ?more green marbles than red marbles. Suppose that there are? $r$ ?red marbles. What is the total number of marbles in the collection?

$mathrm{(A)} 2.85rqquadmathrm{(B)} 3rqquadmathrm{(C)} 3.4rqquadmathrm{(D)} 3.85rqquadmathrm{(E)} 4.25r$

Problem 13

Doug can paint a room in? $5$ ?hours. Dave can paint the same room in? $7$ ?hours. Doug and Dave paint the room together and take a one-hour break for lunch. Let? $t$ ?be the total time, in hours, required for them to complete the job working together, including lunch. Which of the following equations is satisfied by? $t$ ?

$mathrm{(A)} left(frac{1}{5}+frac{1}{7}right)left(t+1right)=1qquadmathrm{(B)} left(frac{1}{5}+frac{1}{7}right)t+1=1qquadmathrm{(C)} left(frac{1}{5}+frac{1}{7}right)t=1\mathrm{(D)} left(frac{1}{5}+frac{1}{7}right)left(t-1right)=1qquadmathrm{(E)} left(5+7right)t=1$

Problem 14

Older television screens have an aspect ratio of? $4: 3$ . That is, the ratio of the width to the height is? $4: 3$ . The aspect ratio of many movies is not? $4: 3$ , so they are sometimes shown on a television screen by "letterboxing" - darkening strips of equal height at the top and bottom of the screen, as shown. Suppose a movie has an aspect ratio of? $2: 1$ ?and is shown on an older television screen with a? $27$ -inch diagonal. What is the height, in inches, of each darkened strip?

$[asy]unitsize(1mm); filldraw((0,0)--(21.6,0)--(21.6,2.7)--(0,2.7)--cycle,grey,black); filldraw((0,13.5)--(21.6,13.5)--(21.6,16.2)--(0,16.2)--cycle,grey,black); draw((0,0)--(21.6,0)--(21.6,16.2)--(0,16.2)--cycle);[/asy]$

$mathrm{(A)} 2qquadmathrm{(B)} 2.25qquadmathrm{(C)} 2.5qquadmathrm{(D)} 2.7qquadmathrm{(E)} 3$

Problem 15

Yesterday Han drove 1 hour longer than Ian at an average speed 5 miles per hour faster than Ian. Jan drove 2 hours longer than Ian at an average speed 10 miles per hour faster than Ian. Han drove 70 miles more than Ian. How many more miles did Jan drive than Ian?

$mathrm{(A)} 120qquadmathrm{(B)} 130qquadmathrm{(C)} 140qquadmathrm{(D)} 150qquadmathrm{(E)} 160$

Problem 16

Points? $A$ ?and? $B$ ?lie on a?circle?centered at? $O$ , and? $angle AOB = 60^circ$ . A second circle is internally?tangent?to the first and tangent to both? $overline{OA}$ ?and? $overline{OB}$ . What is the ratio of the area of the smaller circle to that of the larger circle?

$mathrm{(A)} frac{1}{16}qquadmathrm{(B)} frac{1}{9}qquadmathrm{(C)} frac{1}{8}qquadmathrm{(D)} frac{1}{6}qquadmathrm{(E)} frac{1}{4}$

Problem 17

An equilateral triangle has side length 6. What is the area of the region containing all points that are outside the triangle but not more than 3 units from a point of the triangle?

$mathrm{(A)} 36+24sqrt{3}qquadmathrm{(B)} 54+9piqquadmathrm{(C)} 54+18sqrt{3}+6piqquadmathrm{(D)} left(2sqrt{3}+3right)^2pi\mathrm{(E)} 9left(sqrt{3}+1right)^2pi$

Problem 18

A right triangle has perimeter 32 and area 20. What is the length of its hypotenuse?

$mathrm{(A)} frac{57}{4}qquadmathrm{(B)} frac{59}{4}qquadmathrm{(C)} frac{61}{4}qquadmathrm{(D)} frac{63}{4}qquadmathrm{(E)} frac{65}{4}$

Problem 19

Rectangle? $PQRS$ ?lies in a plane with? $PQ=RS=2$ ?and? $QR=SP=6$ . The rectangle is rotated? $90^circ$ ?clockwise about? $R$ , then rotated? $90^circ$ ?clockwise about the point? $S$ ?moved to after the first rotation. What is the length of the path traveled by point? $P$ ?

$mathrm{(A)} left(2sqrt{3}+sqrt{5}right)piqquadmathrm{(B)} 6piqquadmathrm{(C)} left(3+sqrt{10}right)piqquadmathrm{(D)} left(sqrt{3}+2sqrt{5}right)pi\mathrm{(E)} 2sqrt{10}pi$

Problem 20

Trapezoid? $ABCD$ ?has bases? $overline{AB}$ ?and? $overline{CD}$ ?and diagonals intersecting at? $K$ . Suppose that? $AB = 9$ ,? $DC = 12$ , and the area of? $triangle AKD$ ?is? $24$ . What is the area of trapezoid? $ABCD$ ?

$mathrm{(A)} 92qquadmathrm{(B)} 94qquadmathrm{(C)} 96qquadmathrm{(D)} 98 qquadmathrm{(E)} 100$

Problem 21

A cube with side length? $1$ ?is sliced by a plane that passes through two diagonally opposite vertices? $A$ ?and? $C$ ?and the midpoints? $B$ ?and? $D$ ?of two opposite edges not containing? $A$ ?or? $C$ , as shown. What is the area of quadrilateral? $ABCD$ ?

$[asy] import three; unitsize(3cm); defaultpen(fontsize(8)+linewidth(0.7)); currentprojection=obliqueX; draw((0.5,0,0)--(0,0,0)--(0,0,1)--(0,0,0)--(0,1,0),linetype("4 4")); draw((0.5,0,1)--(0,0,1)--(0,1,1)--(0.5,1,1)--(0.5,0,1)--(0.5,0,0)--(0.5,1,0)--(0.5,1,1)); draw((0.5,1,0)--(0,1,0)--(0,1,1)); dot((0.5,0,0)); label("$A$",(0.5,0,0),WSW); dot((0,1,1)); label("$C$",(0,1,1),NE); dot((0.5,1,0.5)); label("$D$",(0.5,1,0.5),ESE); dot((0,0,0.5)); label("$B$",(0,0,0.5),NW);[/asy]$

$mathrm{(A)} frac{sqrt{6}}{2}qquadmathrm{(B)} frac{5}{4}qquadmathrm{(C)} sqrt{2}qquadmathrm{(D)} frac{5}{8}qquadmathrm{(E)} frac{3}{4}$

Problem 22

Jacob uses the following procedure to write down a sequence of numbers. First he chooses the first term to be 6. To generate each succeeding term, he flips a fair coin. If it comes up heads, he doubles the previous term and subtracts 1. If it comes up tails, he takes half of the previous term and subtracts 1. What is the probability that the fourth term in Jacob's sequence is an integer?

$mathrm{(A)} frac{1}{6}qquadmathrm{(B)} frac{1}{3}qquadmathrm{(C)} frac{1}{2}qquadmathrm{(D)} frac{5}{8}qquadmathrm{(E)} frac{3}{4}$

Problem 23

Two subsets of the set? $S=lbrace a,b,c,d,erbrace$ ?are to be chosen so that their union is? $S$ ?and their intersection contains exactly two elements. In how many ways can this be done, assuming that the order in which the subsets are chosen does not matter?

$mathrm{(A)} 20qquadmathrm{(B)} 40qquadmathrm{(C)} 60qquadmathrm{(D)} 160qquadmathrm{(E)} 320$

Problem 24

Let? $k={2008}^{2}+{2}^{2008}$ . What is the units digit of? $k^2+2^k$ ?

$mathrm{(A)} 0qquadmathrm{(B)} 2qquadmathrm{(C)} 4qquadmathrm{(D)} 6qquadmathrm{(E)} 8$

Problem 25

A round table has radius? $4$ . Six rectangular place mats are placed on the table. Each place mat has width? $1$ ?and length? $x$ ?as shown. They are positioned so that each mat has two corners on the edge of the table, these two corners being end points of the same side of length? $x$ . Further, the mats are positioned so that the inner corners each touch an inner corner of an adjacent mat. What is? $x$ ?

$[asy]unitsize(4mm); defaultpen(linewidth(.8)+fontsize(8)); draw(Circle((0,0),4)); path mat=(-2.687,-1.5513)--(-2.687,1.5513)--(-3.687,1.5513)--(-3.687,-1.5513)--cycle; draw(mat); draw(rotate(60)*mat); draw(rotate(120)*mat); draw(rotate(180)*mat); draw(rotate(240)*mat); draw(rotate(300)*mat); label("(x)",(-1.55,2.1),E); label("(1)",(-0.5,3.8),S);[/asy]$

$mathrm{(A)} 2sqrt{5}-sqrt{3}qquadmathrm{(B)} 3qquadmathrm{(C)} frac{3sqrt{7}-sqrt{3}}{2}qquadmathrm{(D)} 2sqrt{3}qquadmathrm{(E)} frac{5+2sqrt{3}}{2}$

2008AMC10A詳細解析

The machine completes one-third of the job in? $text{11:10}-text{8:30}=text{2:40}$ ?hours. Thus, the entire job is completed in? $3cdot(text{2:40})=text{8:00}$ ?hours.Since the machine was started at? $text{8:30 AM}$ , the job will be finished? $8$ ?hours later, at? $text{4:30 PM}$ . The answer is? $mathrm{(D)}$ .
Since they are asking for the "ratio" of two things, we can say that the side of the square is anything that we want. So if we say that it is? $1$ , then width of the rectangle is? $2$ , and the length is? $4$ , thus making the total area of the rectangle? $8$ . The area of the square is just? $1$ . So the answer is just? $frac{1}{8} times 100 = 12.5 longrightarrow fbox{A}$
$langlelanglelangle 6rangleranglerangle= langlelangle 6ranglerangle = langle 6rangle= 6quadLongrightarrowquadmathrm{(A)}$ Since? $6$ ?is a perfect number, any such operation will yield? $6$ ?as the answer.
If? $frac{2}{3}cdot10 text{bananas}=8 text{oranges}$ , then? $frac{1}{2}cdot5 text{bananas}=left(frac{1}{2}cdot 5 text{bananas}right)cdotleft(frac{8 text{oranges}}{frac{2}{3}cdot10 text{bananas}}right)=3 text{oranges}Longrightarrowmathrm{(C)}$
$frac {8}{4}cdotfrac {12}{8}cdotfrac {16}{12}cdotsfrac {4n + 4}{4n}cdotsfrac {2008}{2004} = frac {1}{4}cdotleft(frac {8}{8}cdotfrac {12}{12}cdotsfrac {4n}{4n}cdotsfrac {2004}{2004}right)cdot 2008 = frac{2008}{4} =$ ? $502 Rightarrow B$ .Notice that everything cancels out except for? $2008$ ?in the numerator and? $4$ ?in the denominator.Thus, the product is? $frac{2008}{4}=502$ , and the answer is? $textbf{(B)}$ .
Let? $d$ ?be the length of one segment of the race.Average speed is total distance divided by total time. The total distance is? $3d$ , and the total time is? $fraclzercpv3jxo{3}+fraclzercpv3jxo{20}+fraclzercpv3jxo{10}=frac{29d}{60}$ .Thus, the average speed is? $3ddivleft(frac{29d}{60}right)=frac{180}{29}$ . This is closest to? $6$ , so the answer is? $mathrm{(D)}$ .
Simplifying, we get $[frac{3^{4016}-3^{4012}}{3^{4014}-3^{4010}}.]$ Factoring out? $3^{4012}$ ?on the top and factoring out? $3^{4010}$ ?on the bottom gives us $[frac{(3^4-1)(3^{4012})}{(3^4-1)(3^{4010})}.]$ Canceling out? $3^4-1$ ?gives us? $frac{3^{4012}}{3^{4010}}=frac{3^2}{3^0}=9.$
Let the sticker price be? $x$ .The price of the computer is? $0.85x-90$ ?at store? $A$ , and? $0.75x$ ?at store? $B$ .Heather saves? $$$$ $15$ ?at store? $A$ , so? $0.85x-90+15=0.75x$ .Solving, we find? $x=750$ , and the thus answer is? $mathrm{(A)}$ .The? $textdollar 90$ ?in store? $A$ ?is? $textdollar 15$ ?better than the additional? $10%$ ?off at store? $B$ .Thus the? $10%$ ?off is equal to? $textdollar 90$ ?-? $textdollar 15$ ? $=$ ? $textdollar 75$ , and therefore the sticker price is? $textdollar 750$ .
$[frac{2x}{3}-frac{x}{6}quadLongrightarrowquadfrac{4x}{6}-frac{x}{6}quadLongrightarrowquadfrac{3x}{6}quadLongrightarrowquadfrac{x}{2}]$ For? $frac{x}{2}$ ?to be an integer,? $x$ ?must be even, but not necessarily divisible by? $3$ . Thus, the answer is? $mathrm{(B)}$ .
Since the area of the large square is? $16$ , the side equals? $4$ ?and if you bisect all of the sides, you get a square of side length? $2sqrt{2}$ ?thus making the area? $8$ . If we repeat this process again, we notice that the area is just half that of the previous square, so the area of? $S_{3} = 4 longrightarrow fbox{E}$ Since the length ratio is? $frac{1}{sqrt{2}}$ , then the area ratio is? $frac{1}{2}$ ?(since the area ratio between two 2-dimensional objects is equal to the side ratio of those objects squared). This means that? $S_2 = 8$ ?and? $S_3 = boxed{textbf{(E) }4}$ .
It will take? $frac{1}{4}$ ?of an hour or? $15$ ?minutes to get to shore.Since only? $30$ ?gallons of water can enter the boat, only? $frac{30}{15}=2$ ?net gallons can enter the boat per minute.Since? $10$ ?gallons of water enter the boat each minute, LeRoy must bail? $10-2=8$ ?gallons per minute? $Rightarrowmathrm{(D)}$ .
The number of blue marbles is? $frac{4}{5}r$ , the number of green marbles is? $frac{8}{5}r$ , and the number of red marbles is? $r$ .Thus, the total number of marbles is? $frac{4}{5}r+frac{8}{5}r+r=3.4r$ , and the answer is? $mathrm{(C)}$ .
Doug can paint? $frac{1}{5}$ ?of a room per hour, Dave can paint? $frac{1}{7}$ ?of a room in an hour, and the time they spend working together is? $t-1$ .Since rate times time gives output,? $left(frac{1}{5}+frac{1}{7}right)left(t-1right)=1 Rightarrow mathrm{(D)}$ If one person does a job in? $a$ ?hours and another person does a job in? $b$ ?hours, the time it takes to do the job together is? $frac{ab}{a+b}$ ?hours.Since Doug paints a room in 5 hours and Dave paints a room in 7 hours, they both paint in? $frac{5*7}{5+7} = frac{35}{12}$ ?hours. They also take 1 hour for lunch, so the total time? 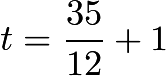$t = frac{35}{12} + 1$ ?hours.Looking at the answer choices,? $(D)$ ?is the only one satisfied by? 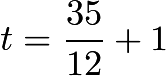$t = frac{35}{12} + 1$ .
Let the width and height of the screen be? $4x$ ?and? $3x$ ?respectively, and let the width and height of the movie be? $2y$ ?and? $y$ ?respectively.By the?Pythagorean Theorem, the diagonal is? $sqrt{(3x)^2+(4x)^2}=5x = 27$ . So? $x=frac{27}{5}$ .Since the movie and the screen have the same width,? $2y=4xRightarrow y=2x$ .Thus, the height of each strip is? $frac{3x-y}{2}=frac{3x-2x}{2}=frac{x}{2}=frac{27}{10}=2.7Longrightarrowmathrm{(D)}$ .
We let Ian's speed and time equal? $I_s$ ?and? $I_t$ , respectively. Similarly, let Han's and Jan's speed and time be? $H_s$ ,? $H_t$ ,? $J_s$ ,? $J_t$ . The problem gives us 5?equations: $2008AMC10A真題與答案解析$ Substituting? $(1)$ ?and? $(2)$ ?equations into? $(5)$ ?gives: $[(I_s+5)(I_t+1)=I_s I_t+70 Longrightarrow I_s I_t+I_s+5I_t+5=I_s I_t+70 Longrightarrow I_s+5I_t=65 quad (*)]$ We are asked the difference between Jan's and Ian's distances, or $[J_s J_t-I_s I_t=x,]$ Where? $x$ ?is the difference between Jan's and Ian's distances and the answer to the problem. Substituting? $(3)$ ?and? $(4)$ ?equations into this equation gives: $[(I_s+10)(I_t+2)-I_s I_t=x Longrightarrow I_s I_t+2I_s+10I_t+20-I_s I_t=x Longrightarrow]$
$[2I_s+10I_t+20=x Longrightarrow 2(I_s+5I_t)+20=x]$

Substituting? $(*)$ ?into this equation gives:

$[2(65)+20=x Longrightarrow 130+20=x Longrightarrow 150=x]$

Therefore, the answer is? $150$ ?miles or? $boxed{mathrm{(D)}}$ .

Let Ian drive? $D$ ?miles, at a speed of? $R$ , for some time(in hours)? $T$ . Hence, we have? $D=RT$ . We can find a similar equation for Han, who drove? $D + 70$ ?miles, at a rate of? $R+5$ , for? $T+1$ ?hours, giving us? $D + 70 = (R + 5)(T + 1)$ . We can do the same for Jan, giving us? $D + x = (R + 10)(T + 2)$ , where? $x$ ?is how much further Jan traveled than Ian. We now have three equations: $[D= RT]$ $[D + 70 = (R+5)(T+1) = RT + R + 5T + 5]$ $[D + x = (R + 10)(T + 2) = RT + 10 T + 2R + 20.]$ Substituting? $RT$ ?for? $D$ ?in the second and third equations and cancelling gives us: $[70 = 5T + R + 5 Longrightarrow 5T + R = 65]$ $[x = 10T + 2R + 20 Longrightarrow x = 2(5T + R ) + 20 Longrightarrow x= 2(65) + 20 = 150.]$ Since? $x = 150$ , our answer is? $boxed{mathrm{D}}$ .
$[asy]size(200); defaultpen(fontsize(10)); pair O=(0,0), A=(3,0), B=(3/2,3/2*3^.5), C=(3^.5,1), D=(3^.5,0), F=(1.5*3^.5,1.5); picture p = new picture; draw(p,Circle(O,0.2)); clip(p,O--C--A--cycle); add(p); draw(Circle(O,3)); dot(A); dot(B); dot(C); dot(O); draw(A--O--B); draw(O--C--D); draw(C--F); draw(D-(0.2,0)--D-(0.2,-0.2)--D-(0,-0.2)); draw(Circle(C,1)); label("(30^{circ})",(0.65,0.15),O); label("(r)",(C+D)/2,E); label("(2r)",(O+C)/2,NNE); label("(O)",O,SW); label("(r)",(C+F)/2,SE); label("(R)",(O+A)/2-(0,0.3),S); label("(P)",C,NW); label("(Q)",D,SE);[/asy]$ Let? $P$ ?be the center of the small circle with radius? $r$ , and let? $Q$ ?be the point where the small circle is?tangent?to? $OA$ . Also, let? $C$ ?be the point where the small circle is tangent to the big circle with radius? $R$ .Then? $PQO$ ?is a right triangle, and a? $30-60-90$ ?triangle at that. Therefore,? $OP=2PQ$ .Since? $OP=OC-PC=OC-r=R-r$ , we have? $R-r=2PQ$ , or? $R-r=2r$ , or? $frac{1}{3}=frac{r}{R}$ .Then the ratio of areas will be? $frac{1}{3}$ ?squared, or? $frac{1}{9}Rightarrow boxed{text{B}}$ .
$[asy] pointpen = black; pathpen = black+linewidth(0.7); pen d = linetype("6 6")+linewidth(0.7); pair A=(0,0),B=(6,0),C=6*expi(-pi/3); D(arc(A,3,90,210)); D(arc(B,3,-30,90)); D(arc(C,3,210,330)); D(arc(A,-3,90,210),d); D(arc(B,-3,-30,90),d); D(arc(C,-3,210,330),d); D(D(A)--D(B)--D(C)--cycle,linewidth(1)); D(A--(0,3)--(6,3)--B); D(A--3*expi(7/6*pi)--C+3*expi(7/6*pi)--C); D(B--B+3*expi(11/6*pi)--C+3*expi(11/6*pi)--C); MP("3",(0,1.5),W); MP("6",(3,0),NW); [/asy]$ The region described contains three rectangles of dimensions? $3 times 6$ , and three? $120^{circ}$ ?degree arcs of circles of?radius? $3$ . Thus the answer is $[3(3 times 6) + 3 left( frac{120^{circ}}{360^{circ}} times 3^2 piright) = 54 + 9pi Longrightarrow mathrm{(B)}.]$
Let the legs of the triangle have lengths? $a,b$ . Then, by the?Pythagorean Theorem, the length of the hypotenuse is? $sqrt{a^2+b^2}$ , and the area of the triangle is? $frac 12 ab$ . So we have the two equations $a+b+sqrt{a^2+b^2} = 32 \\ frac{1}{2}ab = 20$ Re-arranging the first equation and squaring, $sqrt{a^2+b^2} = 32-(a+b)\\ a^2 + b^2 = 32^2 - 64(a+b) + (a+b)^2\\ a^2 + b^2 + 64(a+b) = a^2 + b^2 + 2ab + 32^2\\ a+b = frac{2ab+32^2}{64}$ From? $(2)$ ?we have? $2ab = 80$ , so $a+b = frac{80 + 32^2}{64} = frac{69}{4}.$ The length of the hypotenuse is? $p - a - b = 32 - frac{69}{4} = frac{59}{4}boxed{ mathrm{(B)}}$ .From the formula? $A = rs$ , where? $A$ ?is the area of a triangle,? $r$ ?is its?inradius, and? $s$ ?is the?semiperimeter, we can find that? $r = frac{20}{32/2} = frac{5}{4}$ . It is known that in a right triangle,? $r = s - h$ , where? $h$ ?is the hypotenuse, so? $h = 16 - frac{5}{4} = frac{59}{4}$ .From the problem, we know that $begin{align*} a+b+c &= 32 \ 2ab &= 80. \ end{align*}$ Subtracting? $c$ ?from both sides of the first equation and squaring both sides, we get $begin{align*} (a+b)^2 &= (32 - c)^2\ a^2 + b^2 + 2ab &= 32^2 + c^2 - 64c.\ end{align*}$ Now we substitute in? $a^2 + b^2 = c^2$ ?as well as? $2ab = 80$ ?into the equation to get
$begin{align*} 80 &= 1024 - 64c\ c &= frac{944}{64}. end{align*}$ Further simplification yields the result of? $frac{59}{4}$ .

Let? $a$ ?and? $b$ ?be the legs of the triangle, and? $c$ ?the hypotenuse.

Since the area is 20, we have? $frac{1}{2}ab = 20 => ab=40$ .

Since the perimeter is 32, we have? $a + b + c = 32$ .

The Pythagorean Theorem gives? $c^2 = a^2 + b^2$ .

This gives us three equations with three variables:

$ab = 40 \ a + b + c = 32 \ c^2 = a^2 + b^2$ Rewrite equation 3 as? $c^2 = (a+b)^2 - 2ab$ . Substitute in equations 1 and 2 to get? $c^2 = (32-c)^2 - 80$ .

$c^2 = (32-c)^2 - 80 \\ c^2 = 1024 - 64c + c^2 - 80 \\ 64c = 944 \\ c = frac{944}{64} = frac{236}{16} = frac{59}{4}$ .The answer is choice (B).

Let? $a$ ,? $b$ , and? $c$ ?be the sides of the triangle, with? $c$ ?as the hypotenuse.

We know that? $a + b + c =32$ .

According to the Pythagorean Theorem, we have? $a^2 + b^2 = c^2$ .

We also know that? $ab$ ?= 40, since the area of the triangle is 20.

We substitute? $2ab$ ?into? $a^2 + b^2 = c^2$ ?to get? $(a+b)^2 = c^2 + 80$ .

Moving the? $c^2$ ?to the left, we again rewrite to get? $(a+b+c)(a+b-c) = 80$ .

We substitute our value of 32 for? $a+b+c$ ?twice into our equation and subtract to get? $a + b = frac{69}{4}$ .

Finally, subtracting this from our original value of 32, we get? $frac{59}{4}$ , or? $B$ .
$[asy] size(220);pathpen=black+linewidth(0.65);pointpen=black; /* draw in rectangles */ D(MP("R",(0,0))--MP("Q",(-6,0))--MP("P",(-6,2),N)--MP("S",(0,2),NW)--cycle); D((0,0)--MP("Q'",(0,6),SW)--MP("P'",(2,6),SE)--MP("S'",(2,0))--cycle); D(MP("R''",(2,2),NE)--MP("Q''",(8,2),N)--MP("P''",(8,0))--(2,0)--cycle); D(arc((0,0),(2,6),(-6,2)),dashed);D(arc((2,0),(8,0),(2,6)),dashed);D((2,6)--(0,0)--(-6,2),dashed); D(rightanglemark((2,6),(0,0),(-6,2),12));D(rightanglemark((2,6),(2,0),(8,0),12)); MP("2",(-6,1),W);MP("6",(-3,0),S); [/asy]$ We let? $P'Q'R'S'$ ?be the first rectangle after the rotation, and? $P''Q''R''S''$ ?be the second rectangle after rotation. Point? $P$ ?pivots about? $R$ ?in an?arc?of a circle of radius? $sqrt{2^2+6^2} = 2sqrt{10}$ , and since? $angle PRS,, angle P'RQ'$ ?are complementary, it follows that the arc has a degree measure of? $90^{circ}$ ?(or? $1/4$ ?of the?circumference). Thus,? $P$ ?travels? $frac 14 left(4sqrt{10}right)pi = sqrt{10}pi$ ?in the first rotation.Similarly, in the second rotation,? $P$ ?travels in a? $90^{circ}$ ?arc about? $S'$ , with the radius being? $6$ . It travels? $frac 14(12)pi = 3pi$ . Therefore, the total distance it travels is? $left(3+sqrt{10}right)pi mathrm{(C)}$ .
$[asy] pointpen = black; pathpen = black + linewidth(0.62); /* cse5 */ pen sm = fontsize(10); /* small font pen */ pair D=(0,0),C=(12,0), K=(7,16/3); /* note that K.x is arbitrary, as generator for A,B */ pair A=7*K/4-3*C/4, B=7*K/4-3*D/4; D(MP("A",A,N)--MP("B",B,N)--MP("C",C)--MP("D",D)--A--C);D(B--D);D(A--MP("K",K)--D--cycle,linewidth(0.7)); MP("9",(A+B)/2,N,sm);MP("12",(C+D)/2,sm);MP("24",(A+D)/2+(1,0),E); [/asy]$ Since? $overline{AB} parallel overline{DC}$ ?it follows that? $triangle ABK sim triangle CDK$ . Thus? $frac{KA}{KC} = frac{KB}{KD} = frac{AB}{DC} = frac{3}{4}$ .We now introduce the concept of?area ratios: given two triangles that share the same height, the ratio of the areas is equal to the ratio of their bases. Since? $triangle AKB, triangle AKD$ ?share a common?altitude?to? $overline{BD}$ , it follows that (we let? $[triangle ldots]$ ?denote the area of the triangle)? $frac{[triangle AKB]}{[triangle AKD]} = frac{KB}{KD} = frac{3}{4}$ , so? $[triangle AKB] = frac{3}{4}(24) = 18$ . Similarly, we find? $[triangle DKC] = frac{4}{3}(24) = 32$ ?and? $[triangle BKC] = 24$ .Therefore, the area of? $ABCD = [AKD] + [AKB] + [BKC] + [CKD] = 24 + 18 + 24 + 32 = 98 mathrm{(D)}$ .
$[asy] import three; unitsize(3cm); defaultpen(fontsize(8)+linewidth(0.7)); currentprojection=obliqueX; triple A=(0.5,0,0),C=(0,1,1),D=(0.5,1,0.5),B=(0,0,0.5); draw((0.5,0,0)--(0,0,0)--(0,0,1)--(0,0,0)--(0,1,0),linetype("4 4")); draw((0.5,0,1)--(0,0,1)--(0,1,1)--(0.5,1,1)--(0.5,0,1)--(0.5,0,0)--(0.5,1,0)--(0.5,1,1)); draw((0.5,1,0)--(0,1,0)--(0,1,1)); dot((0.5,0,0)); label("$A$",A,WSW); dot((0,1,1)); label("$C$",C,NNE); dot((0.5,1,0.5)); label("$D$",D,ESE); dot((0,0,0.5)); label("$B$",B,NNW); draw(B--C--A--B--D,linetype("4 4")); draw(A--D--C); [/asy]$ Since? $AB = AD = CB = CD = sqrt{frac{1}{2}^2+1^2}$ , it follows that? $ABCD$ ?is a?rhombus. The area of the rhombus can be computed by the formula? $A = frac 12 d_1d_2$ , where? $d_1,,d_2$ ?are the diagonals of the rhombus (or of a?kite?in general).? $BD$ ?has the same length as a face diagonal, or? $sqrt{1^2 + 1^2} = sqrt{2}$ .? $AC$ ?is a space diagonal, with length? $sqrt{1^2+1^2+1^2} = sqrt{3}$ . Thus? $A = frac 12 times sqrt{2} times sqrt{3} = frac{sqrt{6}}{2} mathrm{(A)}$ .
We construct a tree showing all possible outcomes that Jacob may get after? $3$ ?flips; we can do this because there are only 8 possibilities: $[6quadbegin{cases} text{H}: 11 &quad begin{cases} text{H}: 21 &quad begin{cases} text{H}: boxed{41}\ text{T}: 9.5 end{cases}\ text{T}: 4.5 &quad begin{cases} text{H}: boxed{8}\ text{T}: 1.25 end{cases} end{cases}\ text{T}: 2 &quad begin{cases} text{H}: 3 &qquad! begin{cases} text{H}: boxed{5}\ text{T}: 0.5 end{cases}\ text{T}: 0 &qquad! begin{cases} text{H}: boxed{-1}\ text{T}: boxed{-1} end{cases} end{cases} end{cases}]$ There is a? $frac{5}{8}$ ?chance that Jacob ends with an integer, so the answer is? $mathrm{(D)}$ .
First choose the two letters to be repeated in each set.? $dbinom{5}{2}=10$ . Now we have three remaining elements that we wish to place into two separate subsets. There are? $2^3 = 8$ ?ways to do so (Do you see why? It's because each of the three remaining letters can be placed either into the first or second subset. Both of those subsets contain the two chosen elements, so their intersection is the two chosen elements). Unfortunately, we have over-counted (Take for example? $S_{1} = {a,b,c,d }$ ?and? $S_{2} = {a,b,e }$ ). Notice how? $S_{1}$ ?and? $S_{2}$ ?are interchangeable. A simple division by two will fix this problem. Thus we have: $dfrac{10 times 8}{2} = 40 implies boxed{text{B}}$ Another way of looking at this problem is to break it down into cases.First, our two subsets can have 2 and 5 elements. The 5-element subset (aka the set) will contain the 2-element subset. There are? $dbinom{5}{2}=10$ ?ways to choose the 2-element subset. Thus, there are? $10$ ?ways to create these sets.Second, the subsets can have 3 and 4 elements.? $3+4=7$ ?non-distinct elements.? $7-5=2$ ?elements in the intersection. There are? $dbinom{5}{3}=10$ ?ways to choose the 3-element subset. For the 4-element subset, two of the elements must be the remaining elements (not in the 3-element subset). The other two have to be a subset of the 3-element subset. There are? $dbinom{3}{2}=3$ ?ways to choose these two elements, which means there are 3 ways to choose the 4-element subset. Therefore, there are? $10cdot3=30$ ?ways to choose these sets.This leads us to the answer: $10+30=40 implies boxed{textbf{(B) 40}}$ We label the subsets subset 1 and subset 2. Suppose the first subset has? $k$ ?elements where? $k<5.$ ?The second element has? $5-k$ ?elements which the first subset does not contain (in order for the union to be the whole set). Additionally, the second set has 2 elements in common with the first subset. Therefore the number of ways to choose these sets is? $binom{5}{k} cdot binom{k}{2}.$ ?Computing for? $k<5$ ?we have? $10+30+30+10=80.$ ?Divide by 2 for order to get? $40.$
There are? $dbinom{5}{2}=10$ ?ways to choose the 2 shared elements. We now must place the 3 remaining elements into the subsets. Using stars and bars, we can notate this as: IIIX=>? $dbinom{4}{3}=4$ . Thus,? $4*10=boxed{textbf{(B) 40}}$
$k equiv 2008^2 + 2^{2008} equiv 8^2 + 2^4 equiv 4+6 equiv 0 pmod{10}$ .So,? $k^2 equiv 0 pmod{10}$ . Since? $k = 2008^2+2^{2008}$ ?is a multiple of four and the units digit of powers of two repeat in cycles of four,? $2^k equiv 2^4 equiv 6 pmod{10}$ .Therefore,? $k^2+2^k equiv 0+6 equiv 6 pmod{10}$ . So the units digit is? $6 Rightarrow boxed{D}$ .
Let one of the mats be? $ABCD$ , and the center be? $O$ ?as shown: $[asy]unitsize(8mm); defaultpen(linewidth(.8)+fontsize(8)); draw(Circle((0,0),4)); path mat=(-2.687,-1.5513)--(-2.687,1.5513)--(-3.687,1.5513)--(-3.687,-1.5513)--cycle; draw(mat); draw(rotate(60)*mat); draw(rotate(120)*mat); draw(rotate(180)*mat); draw(rotate(240)*mat); draw(rotate(300)*mat); label("(x)",(-1.55,2.1),E); label("(x)",(0.03,1.5),E); label("(A)",(-3.6,2.5513),E); label("(B)",(-3.15,1.35),E); label("(C)",(0.05,3.20),E); label("(D)",(-0.75,4.15),E); label("(O)",(0.00,-0.10),E); label("(1)",(-0.1,3.8),S); label("(4)",(-0.4,2.2),S); draw((0,0)--(0,3.103)); draw((0,0)--(-2.687,1.5513)); draw((0,0)--(-0.5,3.9686));[/asy]$ Since there are? $6$ ?mats,? $Delta BOC$ ?is?equilateral. So,? $BC=CO=x$ . Also,? $angle OCD = angle OCB + angle BCD = 60^circ+90^circ=150^circ$ .By the?Law of Cosines:? $4^2=1^2+x^2-2cdot1cdot x cdot cos(150^circ) Rightarrow x^2 + xsqrt{3} - 15 = 0 Rightarrow x = frac{-sqrt{3}pm 3sqrt{7}}{2}$ .Since? $x$ ?must be positive,? $x = frac{3sqrt{7}-sqrt{3}}{2} Rightarrow C$ .Draw? $OD$ ?and? $OC$ ?as in the diagram. Draw the altitude from? $O$ ?to? $DC$ ?and call the intersection? $E$ $[asy]unitsize(8mm); defaultpen(linewidth(.8)+fontsize(8)); draw(Circle((0,0),4)); path mat=((-2.687,-1.5513)--(-2.687,1.5513)--(-3.687,1.5513)--(-3.687,-1.5513)--cycle); draw(mat); draw(rotate(60)*mat); draw(rotate(120)*mat); draw(rotate(180)*mat); draw(rotate(240)*mat); draw(rotate(300)*mat); pair D = rotate(300)*(-3.687,1.5513); pair C = rotate(300)*(-2.687,1.5513); pair EE = foot((0.00,0.00),D,C); draw(D--EE--(0,0)); label("(x)",(-1.55,2.1),E); label("(x)",(0.03,1.5),E); label("(A)",(-3.6,2.5513),E); label("(B)",(-3.15,1.35),E); label("(C)",(0.05,3.20),E); label("(D)",(-0.75,4.15),E); label("(O)",(0.00,-0.10),E); label("(1)",(-0.1,3.8),S); label("(4)",(-0.4,2.2),S); draw((0,0)--(0,3.103)); draw((0,0)--(-2.687,1.5513)); draw((0,0)--(-0.5,3.9686)); label("(E)", EE,SE); [/asy]$ As proved in the first solution,? $angle OCD = 150^circ$ . That makes? $Delta OCE$ ?a? $30-60-90$ ?triangle, so? $OE = frac{x}{2}$ ?and? $CE= frac{xsqrt 3}{2}$
Since? $Delta OEC$ ?is a right triangle,? $left({frac{x}{2}}right)^2 + left({frac{xsqrt 3}{2} +1}right)^2 = 4^2 Rightarrow x^2+xsqrt3-15 = 0$

Solving for? $x$ ?gives? $x =frac{3sqrt{7}-sqrt{3}}{2}Rightarrow C$

$[asy]unitsize(8mm); defaultpen(linewidth(.8)+fontsize(8)); draw(Circle((0,0),4)); path mat=(-2.687,-1.5513)--(-2.687,1.5513)--(-3.687,1.5513)--(-3.687,-1.5513)--cycle; draw(mat); draw(rotate(60)*mat); draw(rotate(120)*mat); draw(rotate(180)*mat); draw(rotate(240)*mat); draw(rotate(300)*mat); label("(x)",(-1.95,3),E); label("(A)",(-3.6,2.5513),E); label("(C)",(0.05,3.20),E); label("(E)",(0.40,-3.60),E); label("(B)",(-0.75,4.15),E); label("(D)",(-2.62,1.5),E); label("(F)",(-2.64,-1.43),E); label("(G)",(-0.2,-2.8),E); label("( sqrt{3}x)",(-1.5,-0.5),E); label("(M)",(-2,-0.9),E); label("(O)",(0.00,-0.10),E); label("(1)",(-2.7,2.3),S); label("(1)",(0.1,-3.4),S); label("(8)",(-0.3,0),S); draw((0,-3.103)--(-2.687,1.5513)); draw((0.5,-3.9686)--(-0.5,3.9686));[/asy]$

Looking at the diagram above, we know that? $BE$ ?is a diameter of circle? $O$ ?due to symmetry. Due to Thales' theorem, triangle? $ABE$ ?is a right triangle with? $A = 90 ^circ$ .? $AE$ ?lies on? $AD$ ?and? $GE$ ?because? $BAD$ ?is also a right angle. To find the length of? $DG$ , notice that if we draw a line from? $F$ ?to? $M$ , the midpoint of line? $DG$ , it creates two? $30$ ?-? $60$ ?-? $90$ ?triangles. Therefore,? $MD = MG = frac{sqrt{3}x}{2} Rightarrow DG = sqrt{3}x$ .? $AE = 2 + sqrt{3}x$

Use the Pythagorean theorem on triangle? $ABE$ , we get $[(2+sqrt{3}x)^2 + x^2 = 8^2 Rightarrow 4 + 3x^2 + 4sqrt{3}x + x^2 = 64 Rightarrow x^2 + sqrt{3}x - 15 = 0]$ Using the pythagorean theorem to solve, we get $[x = frac{-sqrt{3} pm sqrt{3 -4(1)(-15)}}{2} = frac{pm 3sqrt{7} - sqrt{3}}{2}]$ $x$ ?must be positive, therefore $[x = frac{3sqrt{7} - sqrt{3}}{2} Rightarrow C]$