參加數學競賽的若干益處

今年我們參加了Math League和AMC (American Math Competition)兩項比賽, 不少學生努力參與嘗試，總體成績較去年取得了一些進步。為了讓更多同學和家長了解這項活動，我總結了一些參加數學學術活動的益處列舉如下，希望今后更多同學能夠參與進來： 磨練技能 數學學術活動是數學課程的延續。準備數學學術活動的過程能夠從廣度和深度上拓展學生的數學知識和技能。

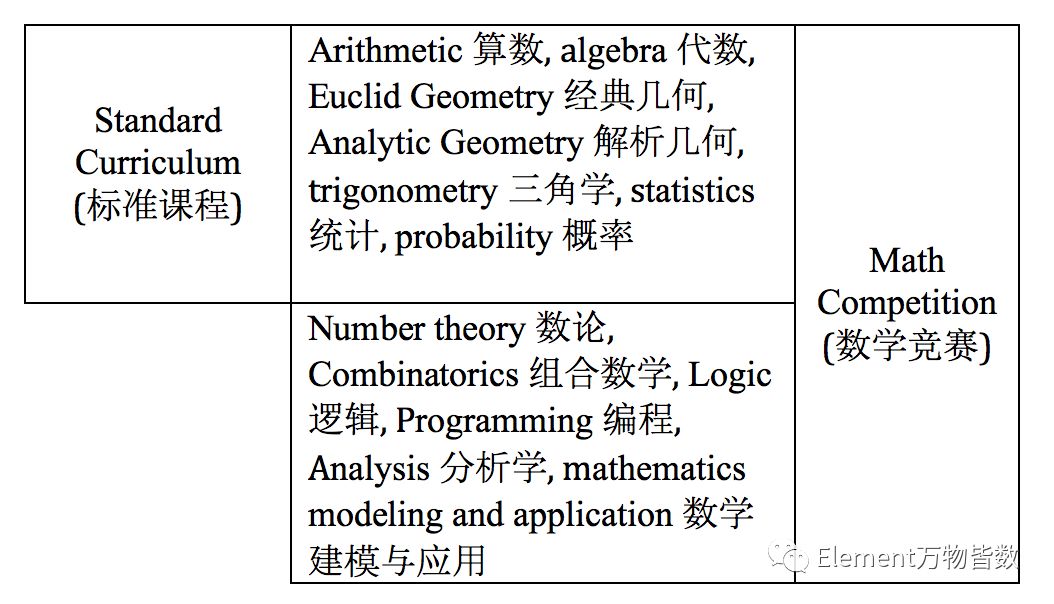
在深度上，數學學術活動也并非“深不可測”，也并非提前學習高年級的內容。靈活運用課內所學就能夠應付絕大部分的學術活動練習。但相比于“一成不變”的課內練習，數學學術活動的習題更耐人尋味，有時考察學生對課內基礎知識的理解，有時需要將不同數學分支的知識結合運用，尋找它們的聯系。
例如：今年數學大聯盟初賽8、9年級的14題

In a regular 10-sided polygon, two pairs of different vertices (four different vertices altogether) are chosen at random, so that all points chosen are distinct from each other. What is the probability that the line segments determined by each pair of points do not interest?
在正十邊形中隨機抽取兩對（四個）不同的頂點。求這兩對頂點相應連成的兩條線段不相交的概率。 從十邊形的十個頂點中任意抽取4個，總共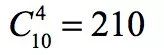 種可能。如果按照正常思路去分析顯然是不明智的。單獨考慮其中一種情況，對于抽取得四個頂點對應連接成的線段，只有以下紅、橙、藍三種可能。 ?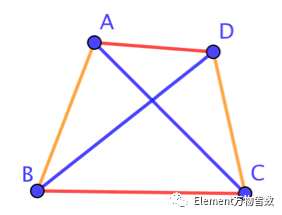
只有AC和BD相交，所以對于這四個點來說相交的概率是2/3。任意四個點被抽中的幾率是等可能的，所以最后答案就是2/3。同樣的問題，選取合適的思路，即使小學生也能夠理解。

按照常規的思路，通常會先去分母把方程化簡為整式，但對于這道題，化簡的結果是 這個結果并不能使我們有很大的收獲。是否還有其他有用的信息我們能夠用到？關鍵在于a, b, c都是正整數以及它們的大小關系。

解決這兩個問題所用的方法都早已在課內的學習中熟稔。劍已在我們手中，就看我們如何去揮舞。

發展認知

數學學術活動的本質是鍛煉學生解決問題的能力(Problem Solving)。學生在分析問題和解決問題的訓練中能夠逐漸培養和運用相應的數學思想。生活中遇到的問題各不相同，但思考問題的方法卻可以遷移參照。

例如解決數學問題常用的“化歸”的思想：是否能夠將目標問題轉化成等價的問題再解決(Sufficient and Necessary)？或者將大問題轉化成若干個小問題再逐個擊破。根據現有條件，我可以推導出什么可利用的信息（Synthesis）？或者從想要取得的結果倒推，我還需要做到什么（Analysis）？
對于很困難的問題，是否有一些特例(Zoom in)，亦或者對于一個問題，我是否能夠找到它更一般的形式（Zoom out）。通常這類問題有什么規律(Induction), 分幾種情況？（classification），我能否將不同對象的關系通過圖表表示出來(Visualization)？問題的本質是什么？在問題中，哪些是變量(Variables)？哪些是不變的(Constant)？

匈牙利數學家波利亞（George Polya）在他的書How to Solve It: A New Aspect of Mathematical Method中對解決問題的方法做了很好的總結。在教育學中有一個概念叫“元認知”(Metacognition)， 即“反思自己如何思考”的意思。

它包括解決問題前的準備(Planning), 解決問題時監控自己的思路(Monitoring)，和解決問題后的反思（Evaluating）。培養學生元認知的能力即是培養他們自主學習的能力。對他們今后的成長和應對新的問題和環境非常關鍵。而數學學術活動中對于解題的訓練能夠使學生的元認知能力得到充分發展。

鍛煉心態

學生在遇到數學難題時往往會經歷復雜的心理變化。從遇到一個有趣的問題時的好奇心，到挑戰難題時的躍躍欲試。而在求解復雜的陌生問題時又會忐忑不安：這么難的問題我是否能夠解出來？

解題中嘗試的過程也是在不斷調整自己心態的過程。在問題被攻克后隨著而來的是強烈而持久的喜悅。在這個過程中，面對困境敢于迎難而上(Grit)，并能夠不懈努力（Perseverance）的品質尤其重要。數學圈流傳著一個笑話：

There are two ways to do great mathematics. The first is to be smarter than everybody else. The second way is to be stupider than everybody else – but persistent.
做數學有兩個途徑：第一個是比所有人都聰明；第二個是比所有人都笨但堅持到底。——Raoul Bott

在數學學術活動中培養的堅韌不拔的精神會成為孩子一生的財富。

助推升學

AMC8是美國初中數學學術活動，是針對八年級一下的數學科測試。它由美國數學協會(Mathematical Association of America, 簡稱MAA)舉辦。每年全球有3000多所名校參與，僅在北美地區，正式登記應試的學生就超過600, 000人次。

此項測驗已經成美國中學校長推介為每年的主要活動之一，是世界上目前信度和效度最高的數學科測試。同系列的的比賽還有AMC10 & 12， 其中表現優異的學生會受邀參加美國數學邀請賽(AIME, American Invitational Mathematics Examination), 為美國數學奧賽國家隊選拔人選參加國際數學奧林匹克學術活動(IMO, International Mathematical Olympiad).

美國“數學大聯盟杯賽”(Math League)是美國及北美地區影響力最大的中小學數學賽事之一。比賽每年舉辦一次，分為初賽、復賽和決賽三個階段。初賽以激發數學學習興趣，培養學生主動探索的精神為主。

復賽的目的是為了啟發學生解決生活中的問題，培養學生創造性思維、批判性思維、和實際解決問題的能力。夏令營和決賽的試題由美國“數學大聯盟杯賽”和普林斯頓大學、哥倫比亞大學、斯坦福大學、紐約州立大學聯合命題，具有很高的挑戰性，是數學超常少年展現才華的絕佳平臺。

享受快樂 除了以上提到的諸多益處，提高學習數學的興趣是參加數學學術活動最大的收獲。 國際數學大會2002年在北京召開，期間著名的數學家陳省身題詞：“數學好玩”。

數學好玩在什么地方？8年級的黃德愷同學有自己獨到的想法： “從因為學好數學會得到來自老師以及家長的夸獎，學習數學的理由一直在變化。直到幾年前，沒有別的很復雜的理由，單純的是數學好玩。

很多人覺得數學很難，很復雜，很枯燥。但其實我覺得數學的趣味性是非常高的。在我眼中，數學仿佛是一只萬能膠，各種毫不相干的東西都能結合起來。雖然這跟數學本來就是因為需要使用而發展出來有關系，但依舊不影響數學的趣味。

當你發現一些貌似毫不相干的知識點背后的原理其實是一樣的時候，那種突破自己腦洞的感覺真的不知如何去形容。比如說楊輝三角，排列組合以及兩數之和的n次方的每一項的系數。這貌似毫不相干的知識點其實是背后有很多的原理是相同的。”

不同的學習階段對“數學好玩”的體會不一樣。“世之奇偉、瑰怪、非常之觀，常在于險遠”，數學好玩在于它的“難”（The challenges of doing math are often its rewards）,在于攻克難關的喜悅，在于發現不同問題背后本質上的聯系的驚喜，在于獲得一個新的有效的視角的收獲，在于應用數學理解生活中實際問題的自豪，也在于欣賞深刻的數學關系和結構的贊嘆。

當代最杰出的數學家陶哲軒(Terence Tao)從小就通過數學學術活動展現了驚異的能力。他8歲半就升入了中學，10歲、11歲、12歲參加國際數學奧林匹克學術活動，分別獲得銅牌、銀牌、金牌。他在Solving Mathematical Problems-A Personal Perspective的前言中說道：

“當我是小學生時，形式運算的抽象美及其令人驚嘆的、通過簡單法則的重復而得出非凡結果的能力吸引了我；當我是高中生時，通過學術活動，我把數學當做一項運動，并享受解答設計巧妙的數學趣味題和解開每一個奧秘的“竅門”時的快樂；當我是大學生時，初次接觸到構成現代數學核心的豐富、深刻、迷人的理論和體系，使我頓起敬畏之心；當我是研究生時，我為擁有自己的研究課題而感到驕傲，并從對以前未解決的問題提供原創性證明的過程中得到無以倫比的滿足。直到自己開始作為一名研究型數學家的職業生涯后，我才開始理解隱藏在現代數學理論和問題背后的直覺力與原動力。”

數學學術活動能讓學生更好地欣賞到數學美，但也可能因為對成績的過度追求導致壓力過大，最終使學生喪失對數學的興趣。純粹的非功利的追求更能夠堅持下去。哪怕知識少學一些，以后還有系統學習的機會。在學習數學學術活動的道路上興趣最重要。只要能夠把對數學的興趣保持下去，就會有不斷探索的欲望。每攻克一道難題，就好像爬上一座山頂，與其糾結于誰爬的山高，不如縱情欣賞山頂一覽無余的美景。

除了以上羅列的幾點，數學學術活動還有很多其他益處。數學學術活動能為有好奇心、愛思考、勇于探索、有恒心的孩子們提供一個進一步學習的平臺，在這個平臺里他們相互一起學習，相互促進，往往能夠迸發出1+1>2的學習效應。