- 翰林提供學術活動、國際課程、科研項目一站式留學背景提升服務!
- 400 888 0080
從特例入手討論AMC12試題
并不是所有學術活動試題的解答都要炫技
有時解題就像生活,要從特殊窺見一般
如何提高數學水平,有時需要小題大做
The 2006 American Mathematics Competition-12 (AMC-12) B exam included the following question:
An object in the plane moves from one lattice point to another. At each step, the object may move one unit up, down, left, or right. If the object starts at the origin and takes a 10-step path, how many different points can be the final point?
平面中的對象從一個格點移動到另一個格點。在每個步驟中,物體可以向上、向下、向左或向右移動一個單元。如果物體從原點開始,走10步的路徑,那么最后一個點可以是多少個不同的點?
這是一個有趣的問題,通過研究它,你會對這里提出的解決方案產生興趣。通過計算1、2和3步之后可以達到多少個點,然后會發現一個規律,從而找到答案。
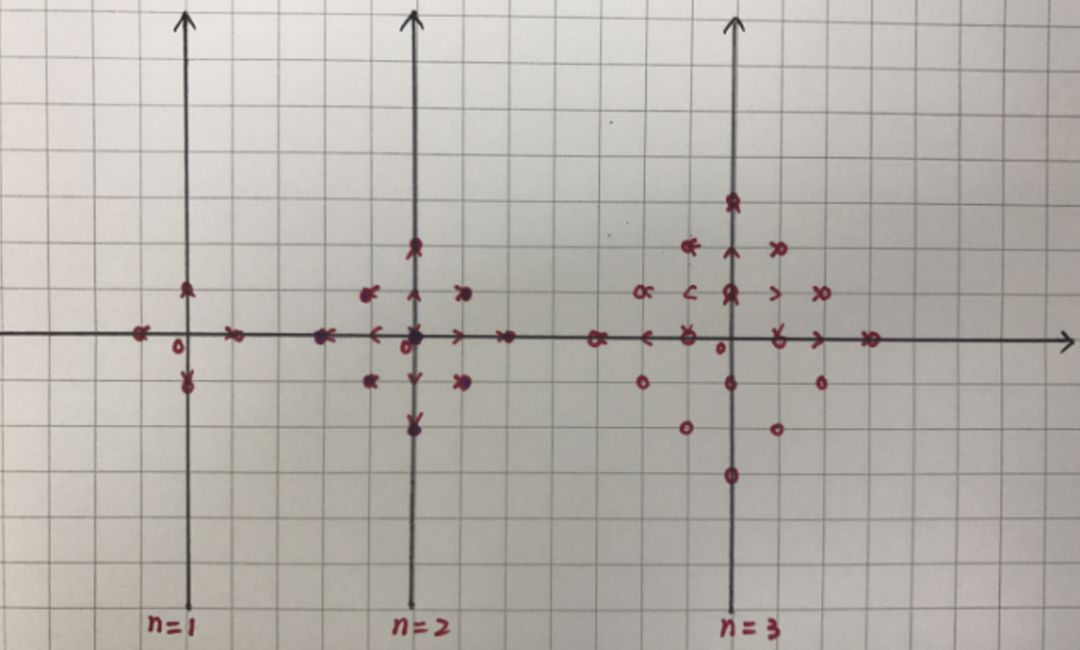
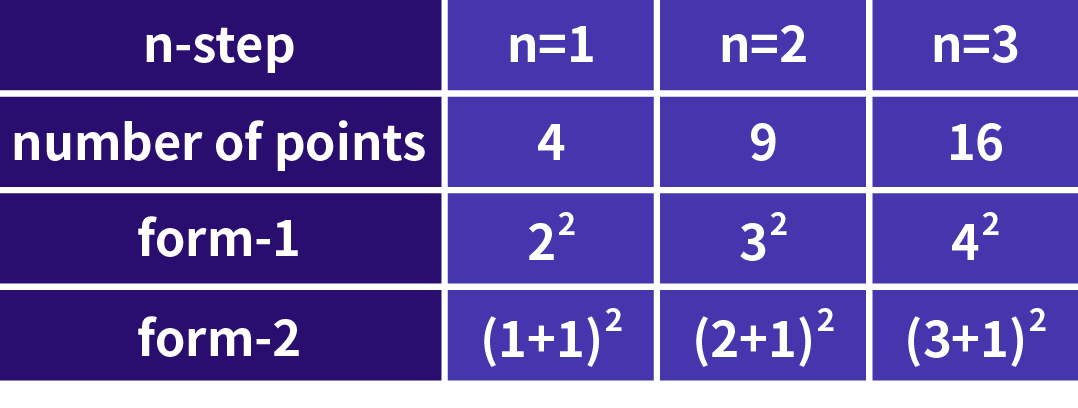
如果你的數字感覺強,你也會用上面這個表格給出的過程進行思考的找到規律的。經過n步,物體可以在(n+1)2個不同的格點,所以問題中要求10步,那么答案就是121。為了比賽的目的,從特例入手解決問題是一個常見的辦法。
可以有人會說這不就是猜嗎,太牽強了吧。那好,我們可以繼續從特例入手,是否可以用到課本教材中常用的分析方法呢。點數的變化,從4開始,依次是9, 16, 25, 36...考慮點數之間的相互關系,用遞推的方法也是可以得出最終的規律。這個方法,我們在學習數列,等差數列時經常用到。
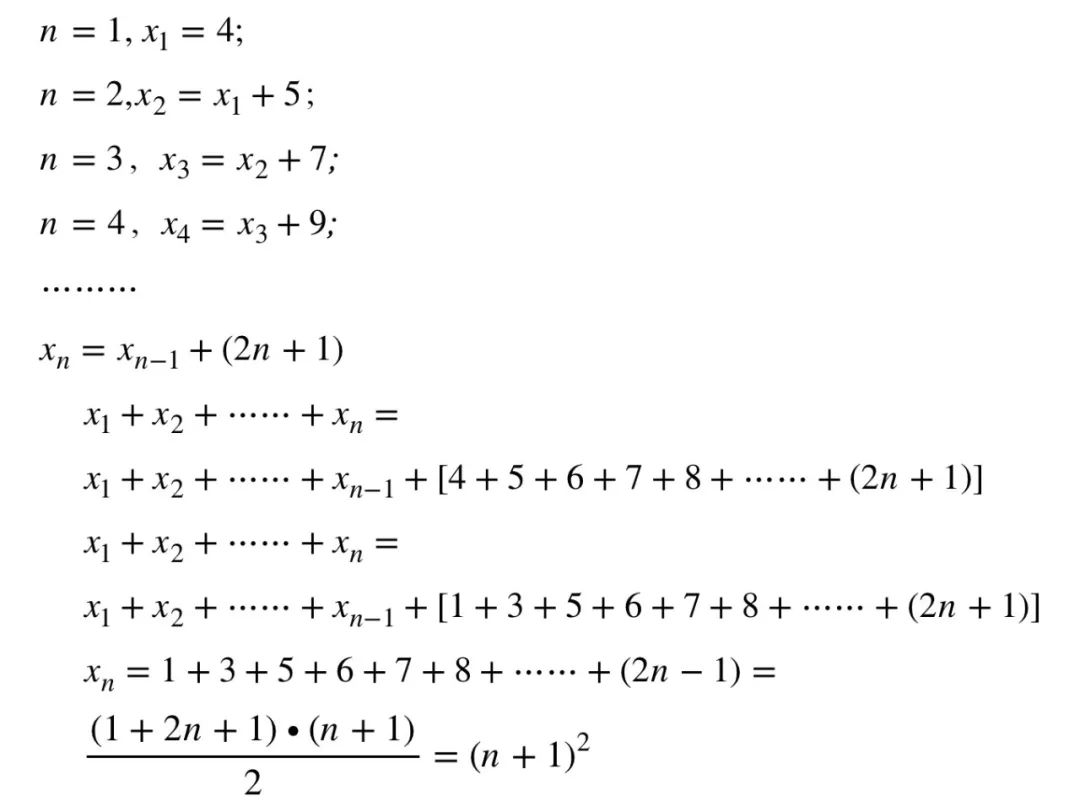
但是上述兩個方法都沒有討論問題中的點是怎么找到的。第一種方法從兩三個簡單的特例入手,發現了規律,在數學上,先看出了規律,在證明的話,我們可以使用課本中講的Mathematical induction,數學歸納法來證明下。
我們還是繼續從特例入手分析,從(0,0)到(1,0)需要的最小步數是1,如果去了又回,出現往返,那步數就多了。因此原點到(x, y)所需的最小步數為(|x|+|y|),因此我們可以找到一個步數n的下邊界,這個下邊界和終點的坐標有一定的關系。這個式子就是通過n步路徑可到達的任何點必須滿足L2(n)的第一個條件。
|x|+|y|<n
因為畢竟是一個在格點上移動的問題,我們來看下每動一次,對點或是位置有什么樣的影響。每次我們從一個格點移動到相鄰格點時,(x+y)的奇偶性要么從偶數變為奇數要么從奇數變為偶數。舉個例子解釋下:從(0,0)到(-2,1)點,最短的步驟就是3步,如果你想2不到達,那真是做夢了。4步不可以,6步不可以,偶數步都不可以。5步,7步,9步,奇數都可以,說明你可以來回走,往返走,兜圈走。上邊的分析,從初等數論的角度出發,我們可以理解為:(x+y)這個坐標的和和步數n(可以的步數)是同模2的,也就是(x+y)和n分別除以2,余數都是相同的。這意味著每個點都可以通過n步路徑實現也滿足下式:
x+y≡n(mod2)
Let L2(n) be the set of lattice points (x, y) in the plane that satisfy?|x|+|y|<n?and x+y=n(mod2).
The original problem, then, asks us to compute how many points are in the set L2(10). We wish to?prove that L2(n) contains (n+l)2?points. Clearly, |L2(1)|=4(where |L2(1)| represents the number of elements in L2(l)), since the points are {(1, 0),(-1, 0), (0, 1), and (0, -1)}. We can likewise verify
that |L2(2)|=9 by listing all 9 points:
L2(2) = {(0, 0), (2, 0), (-2, 0), (0, 2), (0, -2),(1,1),(1,-1),(-1,1),(-1,-1)}
Assume that for k<n, |L2(n)|=(n+l)2.
Now, L2(k+1) is the set of integer solutions to?|x|+|y|<k+1?and x+y=k+1(mod2). Note that the points included in L2(k) will not be solutions for the (k+1)?case, because they have the wrong parity?(even or odd). For instance, the point (k, 0) is in the set L2(k) but not in the set L2(k+1). To proceed by induction, we will need to find a relationship between the (k+l)st?case and previous cases.?We observe that L2(K-1)?L2(K+1).
The points in L2(k+1) that were not already in L2(k-1) are the points whose minimum distance from the origin is exactly k+1, that is
L2(k+1)= L2(k-1)∪{(x,y)||x|+|y|=k+1}
We will count how many points are in the set?{(x,y)||x|+|y|=k+1}?and call this set G2(k+1). First, let us consider the points in quadrant I satisfying the given conditions. These are {(1, k),(2, k-1), (3, k-2),...,(k,1)}. Since there are k points in quadrant I, by the symmetry of the absolute value function, we conclude that there are 4k points not lying on the axes that satisfy the condition. There are 4 points on the axes that we also need to include: (0, k+1), (0, -k-1), (k+1, 0), and (-k-1, 0). This gives us a total of 4k+4 points in the set.
Now, by the inductive hypothesis,?|L2(k-1)|=k2. We have
|L2(k+1)|=k2+4k+4=(k+2)2
翰林AMC12課程體系流程圖

最新發布
? 2025. All Rights Reserved. 滬ICP備2023009024號-1









