11+13+數學考什么｜備戰英國私校入學測試

如果你對英國私校有一定的了解和鉆研，一定會對4+/7+/8+/10+/11+/13+/16+……這些數字不陌生。他們通常對應著英國私校不同年級的入學測試代稱。

比如：

4+ 是Reception入學測試

7+ 是Year 3（三年級）入學測試

以此類推……

那么11+13+對應的正式英國Year 7入學和Year 9入學測試，為什么大家通常會把兩個年級的入學測試放在一起準備呢。那是因為：

1. Year 7的入學測試，通常在Year 6的秋冬季進行。

2. Year 9的入學測試，特別是頂尖公學的Year 9的入學測試也是在Year 6的秋冬季開始第一輪和第二輪的測試。

＊當然，不少女校的Year 9入學測試是在Year 8開始進行

＊頂尖公學的最后一輪測試CE在Year 8進行

＊參加late registration或海外考生可能有不同的考試時間和流程。

但總的來說，在YEAR 6進行的11+測試，和13+的pre-test和第二輪School test是多數考生的兵家必爭之地。

那么這么重要的考試的最重要的科目之一——數學，都考些什么？

從英國教學大綱查找

獲取知識點的第一個途徑是英格蘭教學大綱（National Curriculum in England），這里會列出每個年級需要掌握的知識點。我們以Year 6的Program of Study為例來帶大家看看幾個大的方面，并舉幾個例子看一樣具體要求：

Number（數字） - number and place value

Number - addition, substraction, multification and division加減乘除

Number - fraction (including decimals and percentages)分數和百分數

Ratio and Proportion （比例）

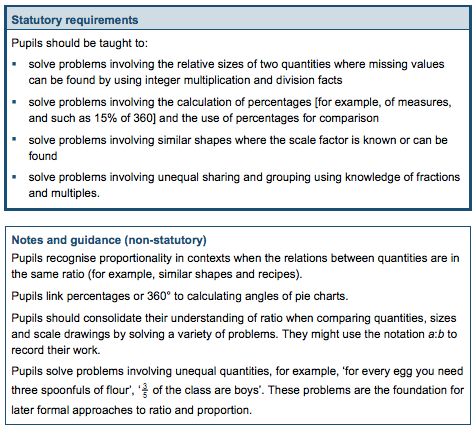
Algebra（代數）

Measurement （度量衡）

Geometry （幾何）- properties of shapes

Geometry - position and direction

Statictics （統計）

但有趣的是，當我們翻看一年級的數學教學大綱，多數大項目和六年級的一樣！只是少了百分數／代數／Ratio and Proportion／統計。可以見英國的大綱是把知識結構先搭建起來，在逐漸細化具體的過程。如朋友所說，就像在做一個雕塑，從粗略的外觀，到一層一層細化打磨，最后成為美麗的藝術品。

在如下英國政府網站上，你可以找到針對各個年級的數學大綱的要求。

https://www.gov.uk/government/publications/national-curriculum-in-england-mathematics-programmes-of-study/national-curriculum-in-england-mathematics-programmes-of-study

從私校考試試卷總結

敲黑板！

所有考試家庭都知道，參加私校數學考試，并不是學透了6年級的知識點就萬事大吉了。尤其是那些熱門頂尖私校，考試的難度都遠遠超過Year 6，從而起到篩選和選拔的作用。那么了解數學考試內容和難度的另一個方法——就是從復習資料和考試試卷里尋找。

常見的復習資料練習冊，可以參考那些知名的英國教輔叢書。

下面我們再以倫敦知名女子中學St Pauls Girls的數學樣卷中的一道題為例，幫大家分析一下它涉及的知識點和考試難度。

題目：

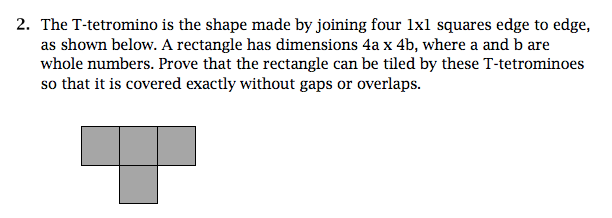
答案：

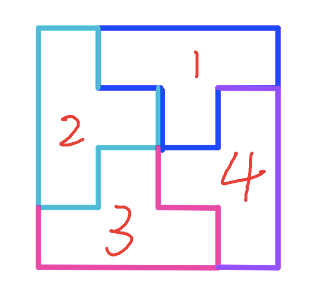
4 T-tetrominos can be arranged

as a 4x4 square

So for a 4a x 4b rectangle, it consists

a rows of (4 x 4) squares

b columns of (4 x 4) squares

Therefore, 4x4 squares form 4a x 4brectangle.? As 4 T-tetrominos can be arranged as a4 x 4 square, hence T-tetrominos can form a 4a x 4b rectangle.

點評：

這道題的數學背景是由美國數學家Solomon W. Golomb教授在1953年提出的多方塊(Polyominoes )理論，并且在1965年出版的著作《多方塊》(Polyominoes)一書中有系統闡述，該理論也是著名游戲“俄羅斯方塊”的數學基礎之一。這道題考察孩子對正方形和矩形面積的理解和代數求證。劉老師在閱卷時，發現很多考生對該題無從下手。其實，題目求證4a x 4b矩形中包含4 x 4，已經暗示和4 x 4正方形相關，然后可以進一步數學猜想，能否從T-tetrominos 組成一個4x4正方形，答案是肯定的，如此倒推即可輕松解答。

這是11+考綱2D shape 的compound shape area 部分，同時也考察對multiple 的理解。在劉老師的11+獎學金班里會涉及到這一類的題目。

根據在中國多年的考試經驗，系統的學習知識點，在做練習的過程中發現薄弱環節進行強化，反復鞏固以達到融會貫通，再加上速度敏捷度，典型題目的熟悉……是一個相對全面完善的復習方案。

最后祝各位考生和家長，都能順利度過11+13+的備考生活，金榜題名！