翰林國際教育，國內國際競賽領域的開拓者與引領者。我們不僅是系統輔導與深度教研的先行者，更為整個行業提供權威的賽事資訊與海量真題講義。在數學、物理、化學、生物、計算機、商科、數模等核心領域，我們的戰績長期穩居頭部領先地位，屢屢斬獲國家隊級別最高榮譽。作為同時擁有學科培訓、AP國際學校及美高資質的權威教育組織，我們為學生提供一站式的卓越培養體系，助力英才邁向世界頂尖學府。

一、體制內升學：中考與高考中的“差異化競爭力”

中考強基計劃中的核心參考價值

國內頂尖中學的“強基計劃”旨在選拔具有理科潛力的學生，AMC10成績成為評估數學能力的關鍵指標。例如，北京人大附中、上海華師大二附中等學校在理科實驗班招生中，明確將AMC10獎項作為面試準入條件。全球排名前5%的獲獎者可直接獲得面試資格，無需經過初試篩選。這一政策表明，AMC10成績不僅代表學生的數學水平，更被視為綜合素質的體現。強基計劃通過此類競賽篩選學生，旨在快速識別具備高階思維能力的潛質人才。

高考綜合評價中的“學術特長”認證

在高考多元錄取機制下，復旦大學、上海交通大學等高校在綜合評價招生中，將AMC10獎項作為學術能力的補充證明。獲獎學生可部分替代傳統學科競賽成績（如數學聯賽），成為“學術特長生”的重要標簽。尤其在江浙滬地區的綜評體系中，AMC10全球前2.5%的獎項被視為省級數學競賽二等獎同等含金量，可直接在申請材料中凸顯學生的數學優勢。這一趨勢反映了國內高校對國際化競賽標準的接納，以及對跨學科思維能力的重視。

競賽背景對學科競爭力的長期增益

體制內學生若在AMC10中晉級AIME（美國數學邀請賽），其數學思維深度將顯著超越同齡人。AMC10的命題邏輯強調抽象推理與問題建模能力，這與國內數學聯賽、物理競賽的考察方向高度契合。獲獎學生在后續競賽中（如全國高中數學聯賽）往往表現更突出，因其已適應高難度、多變式的解題環境。此外，AMC10的訓練能提升學生的邏輯嚴謹性與計算效率，間接助力高考數學壓軸題的攻克。

二、體制外升學：海外名校的“隱性篩選標準”

美國本科申請中的學術能力背書

麻省理工學院（MIT）、加州理工學院等頂尖理工院校在申請系統中明確建議提交AMC10成績。盡管列為“可選”，但實際錄取數據表明，全球前1%的獲獎者中約有30%最終進入TOP20美國高校。這些學校將AMC10成績視為數學潛力的核心指標，其含金量可直接對標中國數學奧林匹克（CMO）省級一等獎。尤其對于申請工程、計算機等專業的學生，AMC10高分可彌補SAT/ACT數學分數的單一性，證明其思維層次遠超標準化考試范圍。

英國G5高校的專業能力評估工具

牛津大學、劍橋大學的數學與計算機專業常在面試中使用AMC10真題測試學生反應速度與思維延展性。帝國理工學院則直接在申請指南中注明，AMC10成績可作為“學術潛力證明”替代部分筆試成績。英國高校重視競賽成績的原因在于，AMC10的題目設計強調邏輯鏈條的完整性與非標準解法，這與英國精英教育中的批判性思維要求高度一致。獲獎者在面試中更易展現其適應高強度學術環境的能力。

國際學校入學與課程體系的銜接優勢

深國交、上海平和學校等知名國際學校在入學考試中直接采用AMC10原題或改編題，獎項獲得者可獲優先錄取資格。這些學校將AMC10成績視為學生適應國際課程（如IB、AP微積分）的關鍵預測指標。據統計，AMC10高分學生在國際課程中的數學科目平均成績比未參與者高15%以上。此外，AMC10的訓練有助于學生提前熟悉西方數學體系的表達方式與論證邏輯，減少未來留學后的學術適應周期。

三、綜合價值：超越升學的思維塑造與長遠影響

AMC10的含金量不僅體現在升學環節，更在于其對思維模式的深層塑造。其題目設計融合了知識應用與創新探索，要求學生突破模板化解題模式，培養多角度分析問題的能力。這種訓練對任何學術方向的學生均有長遠價值：體制內學生可提升理科綜合素養，體制外學生則能構建與國際教育接軌的思維框架。

不同課程體系學生備考AMC10數學競賽規劃

一、體制內學生：補全競賽思維，突破“應用題陷阱”

1.? ? 系統性知識補全

使用《奧數教程》等專業競賽教材，重點學習數論模塊（包括質因數分解、同余方程、整數性質）、組合數學（排列組合進階、容斥原理、鴿巢原理）等AMC10高頻考點

每周安排固定時間學習新知識點，并通過配套習題鞏固理解，建議每日投入1-2小時專項訓練

建立知識圖譜，將離散的知識點系統化，形成完整的數學知識體系

2.? ? 思維模式轉型訓練

從“結果導向”解題轉向“過程導向”分析，重點訓練反證法、數學歸納法等證明方法

通過AMC10歷年真題訓練“一題多解”能力，特別是后10道難題的多種解法分析

參加線上競賽社群，與其他考生交流解題思路，拓寬思維維度

3.? ? 階梯式真題訓練

從AMC8真題入手建立基礎，逐步過渡到AMC10早期真題，最后挑戰近年高難度真題

重點分析2015年后的AMC10真題，總結后10道題的出題規律和解題技巧

掌握“設數法”、“度量法”、“極端原理”等快速解題技巧，提高解題效率

4.? ? 應試策略優化

模擬真實考試環境，每周末進行全真模考，訓練時間分配能力

前15題控制在40分鐘內完成，后10題留出35分鐘深度思考

建立錯題本系統，定期復盤錯誤原因，避免同類錯誤重復發生

二、IB體系學生：深化HL課程，填補“知識斷層”

1.? ? 針對性知識補充

使用《Introduction to Number Theory》系統學習數論基礎，重點掌握模運算、狄利克雷特征等概念

通過《Geometry Revisited》深化幾何理解，特別是圓的性質、三角形幾何和幾何變換

將IB知識體系與AMC10考點對接，例如用IB概率知識解決AMC10中的概率問題

2.? ? 真題模擬與時間管理

每周完成1套完整的AMC10限時模擬，嚴格遵循75分鐘的時間限制

訓練“跳題策略”：遇到卡殼超過3分鐘的題目立即跳過，確保完成所有力所能及的題目

使用計時器分段控制：前10題（20分鐘）、中間10題（25分鐘）、后5題（30分鐘）

3.? ? 跨學科能力整合

將IB物理中的力學問題轉化為數學模型，如用微積分求解極值問題

利用IB的TOK（知識論）訓練批判性思維，提高對數學問題本質的理解

建立數學建模思維，將實際問題抽象為數學問題，這也是IB評估的重要能力

4.? ? 資源優化利用

充分利用IB學校的國際資源，獲取AMC10官方備考材料

參加校內數學社團或創建學習小組，通過同伴學習提高備考效率

利用IB假期時間參加專項培訓營，集中突破薄弱環節

三、A-Level體系學生：查漏補缺，避開“微積分誤區”

1.? ? 基礎能力強化

使用《Algebra and Trigonometry》鞏固代數基礎，重點訓練多項式因式分解、余數定理、二次函數性質等

補充幾何構造訓練，特別是平面幾何的證明方法和立體幾何的空間想象能力

通過Khan Academy等在線平臺彌補知識漏洞，建立完整的知識體系

2.? ? 錯題管理系統

建立電子化錯題本，按知識點分類記錄錯誤題目

標注錯誤類型：計算錯誤、概念錯誤、思路錯誤等，針對性改進

每周回顧錯題，確保同類錯誤不再發生

3.? ? 解題技巧專項訓練

掌握“排除法”、“特殊值法”、“選項代入法”等快速解題技巧

4.? ? 備考節奏規劃

提前3-6個月開始系統備考，分階段制定學習目標

第一階段（1-2個月）：知識點全面覆蓋

第二階段（1-2個月）：真題分類訓練

第三階段（1個月）：全真模考與弱點強化

最終階段（2周）：心理調整與策略優化

四、AP體系學生：知識遷移，發揮“微積分優勢”

1.? ? 前置知識拓展

提前完成AP微積分基礎內容，為后續晉級AIME做準備

重點訓練“微積分與數列結合”的題型，這是AMC10到AMC12的過渡重點

2.? ? 跨學科應用訓練

將微積分思想應用于AMC10最值問題，如幾何面積優化、函數極值求解

用數列知識解決“遞推關系”問題，這是AMC10的常見題型

3.? ? 綜合能力提升

a.? 每周完成2套真題模擬，注重質量而非數量，深度分析每道題的多種解法

b.? 參加線上競賽課程，學習專業競賽教師的解題技巧和思維方法

c.? 建立解題思維框架：問題分析→方法選擇→過程實施→結果驗證

4.? ? 長期發展規劃

將AMC10作為起點，規劃AMC12→AIME→USAMO的晉級路徑

利用AP微積分基礎，提前學習多元微積分和線性代數，為更高層次競賽做準備

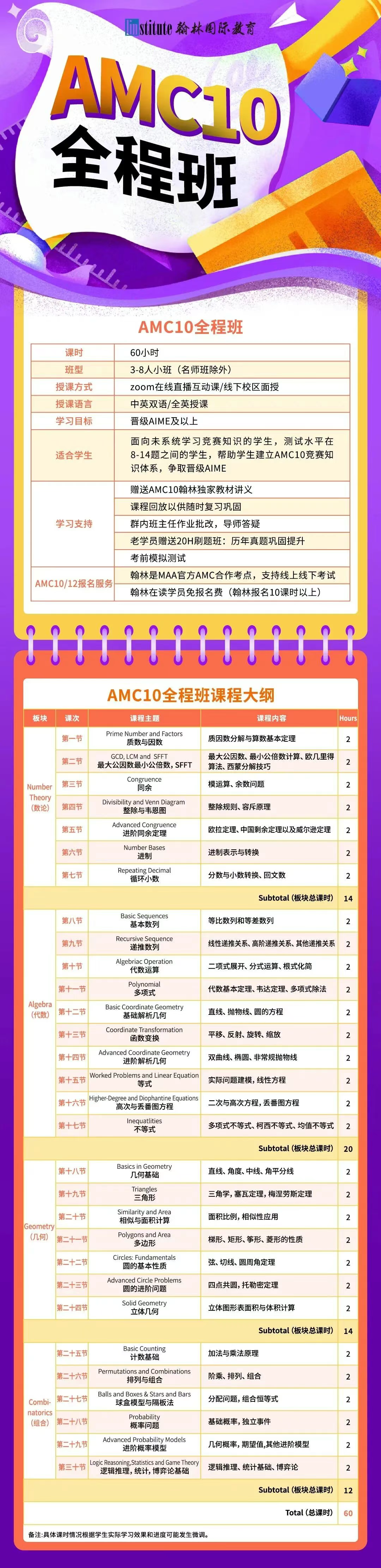
翰林AMC10培訓班

翰林AMC10培訓班