今天下午,2025年上海中考數(shù)學終于塵埃落定。上周的上海高考數(shù)學出乎意料的簡單,那么這次中考難度到底如何呢?
某自媒體做了一個投票,結(jié)果呈現(xiàn)出兩極分化的情況:

有說很簡單,甚至班里幾個同學對了一下都感覺不錯;也有說比24年難,尤其是幾道重點題。


簡單和難,本來就因人而異,但既然出現(xiàn)兩級分化,也說明這一次的中考題出得還是中規(guī)中矩的。
有趣的是,投票的有超過一半的是“吃瓜群眾”,這其中應該不僅有26屆或者其他年級的未來中考候選選手,也有很多關心中考的小學家長。雖然中考離自己的孩子還很遠,甚至很多人連小升初這一關還沒過,但中考無疑是一個風向標。
那么想要把初中數(shù)學學好能在中考中勝出,小學數(shù)學該打好哪些底子呢?小學參加各種數(shù)學競賽,學了很多校外的內(nèi)容,到了初中還有用嗎?
可以說,付出一定有回報,但也有前提!
掃碼添加顧問老師領取
《AMC 8預學全指導(Pre-AMC)》


更多信息可咨詢顧問
小學競賽的內(nèi)容到初中就消失了?
“雞兔同籠學了那么多方法有什么用?到了初中一個方程就搞定了”。這也許是很多家長的困惑。別說用方程就能解決小學里的大部分“難題”,甚至到了初中這樣的文字應用題本身也少了很多。
那么是不是小學競賽里的東西都“白學”了呢?當然不是。其實競賽中的很多內(nèi)容,是在給后續(xù)的學習做鋪墊。
01從具象到抽象的鋪墊
比如小學階段有很多“巧算”題,無論湊整法、基準數(shù)法、重組法等,核心就是運算定律的靈活應用。小學階段學的是“數(shù)”,到了初中階段學的是“式”,雖然對象變了,但運算的規(guī)則沒有變,并且在這個過程中還積累了“數(shù)感”(對數(shù)字關系的敏感直覺)。因此小學階段如果能對運算定律的綜合應用達到融會貫通,那么初中的代數(shù)式運算、因式分解等內(nèi)容的學習會更加輕松。
同樣,行程問題、等量代換等,雖然到了初中似乎都看不到了,但其實只是以動點問題、換元法等更抽象的形式出現(xiàn)了而已。
02從直覺猜想到邏輯論證的鋪墊
盡管我們一直說“數(shù)學講邏輯”,但其實整個小學階段的學習,直覺的占比還是非常高的。舉個例子:
在周長相等的情況下,探索不同長寬矩形的面積變化,小學的主要方式是“歸納推理”,比如利用下面的表,學生可以很直觀地發(fā)現(xiàn)“長寬越接近、面積越大”。但這種結(jié)論并不嚴謹,到了初中學了二次函數(shù)后就能做非常嚴謹?shù)摹把堇[推理”了。
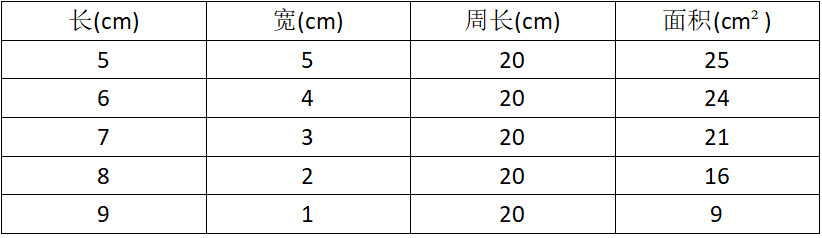
這也是為什么很多孩子到了初中學習會感到不適應的原因,因為初中無論是平面幾何的證明還是代數(shù)式的推導,都要求更嚴謹?shù)倪壿?/span>。
而在我們的競賽思維課程中,其實有非常多的“好用”結(jié)論,這些結(jié)論怎么來的?一個好的老師應該會帶孩子做比較細致的解釋。比如數(shù)論中3的整除性,就需要通過位值原理來嚴格論證。

再比如斐波那契數(shù)列主題中的“爬樓梯”問題,既需要直覺感受數(shù)字規(guī)律,又需要利用遞推的方式一步步發(fā)現(xiàn)規(guī)律背后的秘密。
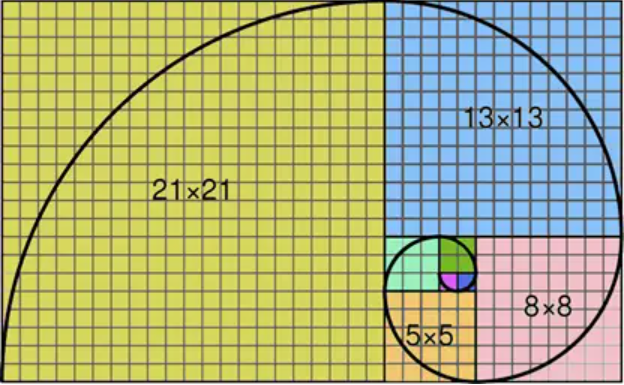
因此,一個“不套路”的競賽課程,是可以提前讓學生了解到“正確做數(shù)學的方式”,并感受數(shù)學的邏輯美感的。
從這三個數(shù)學思想小學務必掌握
競賽一般分為四大模塊:數(shù)論、代數(shù)、幾何、排列組合(國內(nèi)小奧一般歸為七大模塊,但大同小異)。內(nèi)容很多很雜,如果不是未來也走競賽路線,必然有些東西會遺忘甚至以后完全不會碰,但也有一種東西是會貫穿小初高甚至其他學科學習的東西——數(shù)學思想方法。其中有三個在初中學習中最為常用:
01分類思想
分類思想可以說是整個數(shù)理思維的起點,并且貫穿了從幼兒園到大學的全部數(shù)學學習階段。擁有分類思想的學生往往想問題“很全面”,并且能夠“分而治之”。而在初中的數(shù)學學習中無孔不入,甚至開始逐漸成為拉開差距的重點,比如下面的一個簡單問題卻非常容易丟分:
設a、b、c是三個實數(shù),請用a、b、c表示方程ax2+bx+c=0的解
很多同學直接就用一元二次方程的求根公式,但你是否忘了,題目并沒有說這是二次方程啊,所以要分成a=0和a≠0進行討論得到不同答案。這種錯誤看似是“粗心”,其實就是源于概念的細節(jié)沒有把握好,以及沒有分類討論的意識。
分類思想在小學競賽中非常常見,比如低年級熟悉的“數(shù)圖形”問題,想要不漏不重復,最重要的就是要“先分類再數(shù)”。
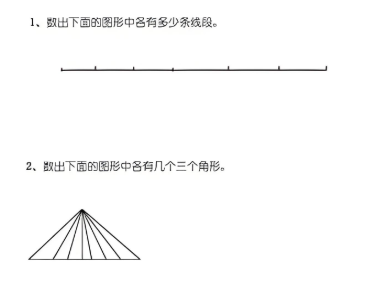
02數(shù)形結(jié)合思想
“數(shù)缺形時少直觀、形缺數(shù)時難入微”,數(shù)形結(jié)合思想也幾乎是可以滲透到每一個數(shù)學概念中的。尤其初中的很多概念越來越抽象,采用數(shù)形結(jié)合就能四兩撥千斤,比如下面這個常見的絕對值化簡問題,看上去是一道代數(shù)題,但利用“絕對值就是距離”這個直觀解釋,這題就變成了“a和b的距離是6、a和c的距離是10”,解起來就很方便了。
已知|a-b|=6,|a-c|=10,求|b-c|=______________
在競賽思維課程中,數(shù)形結(jié)合思想幾乎也是隨時都會出現(xiàn)的,比如在解決“和差倍問題”時,利用線段圖去理解題目;又或者在研究“乘法原理”時用樹狀圖去整理不同分類情況。
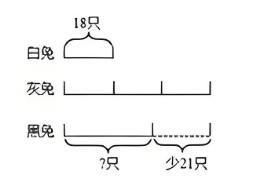
03對應思想
其實從數(shù)數(shù)開始,就已經(jīng)有了對應思想,而初中的一個重點“函數(shù)”,本質(zhì)上就是對應思想的具體化和形象化。
利用對應思想有時候可以“降維打擊”一些數(shù)學問題,比如下面這個問題:
有32個人參加乒乓球比賽,兩兩一組進行單打比賽,贏的人晉級下一輪,輸?shù)闹苯犹蕴U垎栆还残枰嗌俦荣惸墚a(chǎn)生冠軍。
這個問題很多學生拿到就開始進行計算:32÷2=16、16÷2=8......
但其實這個題目只要用對應思想就可以秒解,因為“一場比賽淘汰一個人”,所以32個參賽者需要淘汰31個人,需要31場。
所以,學競賽的孩子到了初中面對更抽象、更復雜的問題,可以說會更加游刃有余,因為即使沒有超前學,內(nèi)容可能陌生,但學習的方法反而會感覺很熟悉。
而競賽帶來的數(shù)學思維培養(yǎng)并非一朝一夕就能形成,好的老師和好的課程就非常關鍵啦。以下是主流低齡國際數(shù)學競賽指南,同學們可以考慮參加哦👇。
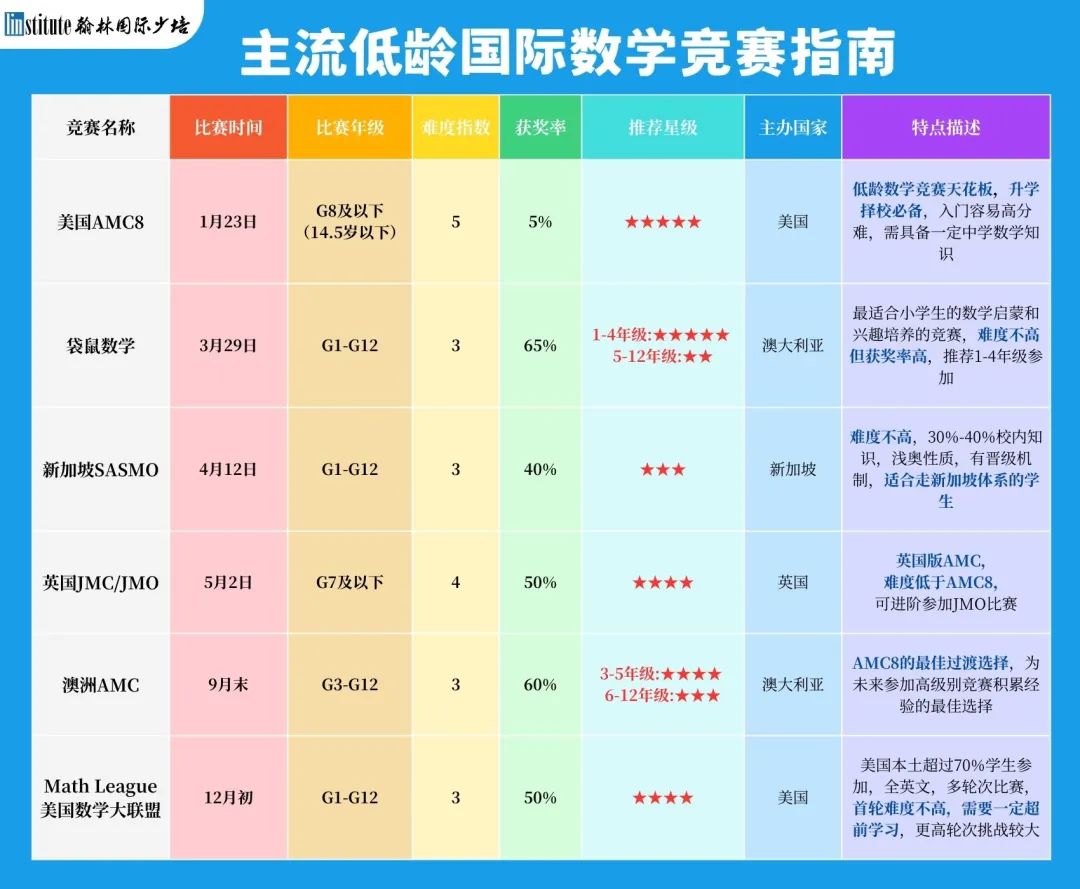
了解更多請掃碼添加顧問老師
同時可以領取:
《AMC 8預學全指導(Pre-AMC)》


更多信息可咨詢顧問
翰林AMC8
全方位課程服務概覽
⏬️⏬️⏬️

往期文章閱讀推薦:










